やること
※2022/09/20修正があります
前回は2次元の迷路における最短経路を求めました。今回は3次元の迷路の最短経路を、幅優先探索で求めてみましょう。
実行環境
WinPython3.6をおすすめしています。
必修科目
18-2の記事を必ず履修し、それと見比べながら今回は実装してください。前回のコードに書き加える形で実装することでより理解が深まります。
import
今回使うパッケージをインポートします。3次元のグラフを表示するため、Axes3Dが追加されました。
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage.filters import minimum_filter, maximum_filter
from mpl_toolkits.mplot3d import Axes3D迷路の作成
今回も手入力です。’#’は壁(=障害物)です。
#########################
# 迷路
#########################
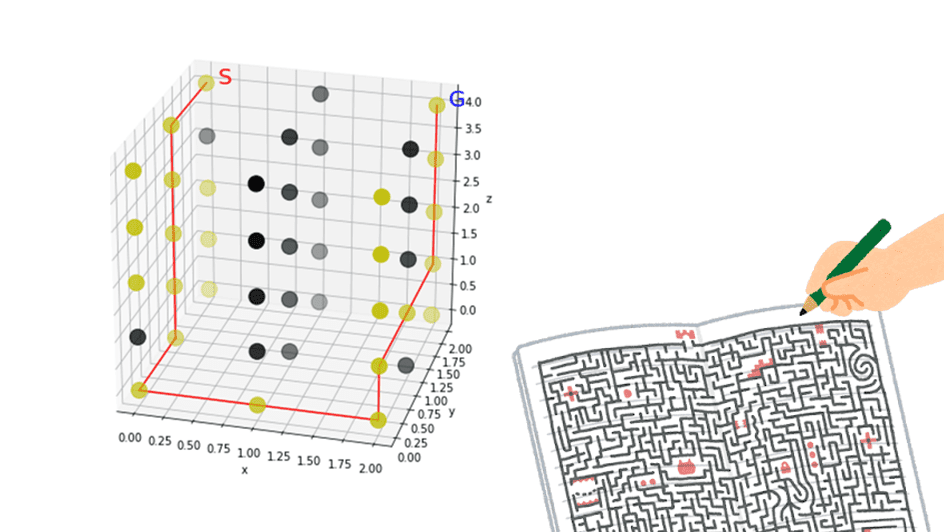
maze = [['-#---',
'-----',
'---#s'],
['-####',
'#####',
'#####'],
['-----',
'#-###',
'----g']]3次元で分かりづらいですが、最短経路はこのようになるはずです。
前処理
前回のコードをごく単純に3次元に拡張しただけです。比べてみるとビックリするかもしれません。
#########################
# 前処理
#########################
#たてとよこ
h, w, l = len(maze), len(maze[0]), len(maze[0][0])
#コスト
cost = np.zeros((h, w, l), dtype=int) + 999
#コストが書き込まれて探索が終了したマス(bool)
done = np.zeros((h, w, l), dtype=bool)
#障害物(bool)
barrier = np.zeros((h, w, l), dtype=bool)
#プーリング用のフィルタ
g = np.array([[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]],
[[0, 1, 0],
[1, 1, 1],
[0, 1, 0]],
[[0, 0, 0],
[0, 1, 0],
[0, 0, 0]]])
#mazeからスタート位置、ゴール位置、障害物位置を取得
for i in range(h):
for j in range(w):
maze[i] = list(maze[i])
for k in range(l):
if maze[i][j][k] == 's':
start = (i, j, k)
cost[i, j, k] = 0
done[i, j, k] = True
if maze[i][j][k] == 'g':
goal = (i, j, k)
if maze[i][j][k] == '#':
barrier[i, j, k] = True
print('start\n{}'.format(start))
print('goal\n{}'.format(goal))
print('cost\n{}'.format(cost))
print('done\n{}'.format(done))
print('barrier\n{}'.format(barrier))start
(0, 2, 4)
goal
(2, 2, 4)
cost
[[[999 999 999 999 999]
[999 999 999 999 999]
[999 999 999 999 0]]
[[999 999 999 999 999]
[999 999 999 999 999]
[999 999 999 999 999]]
[[999 999 999 999 999]
[999 999 999 999 999]
[999 999 999 999 999]]]
done
[[[False False False False False]
[False False False False False]
[False False False False True]]
[[False False False False False]
[False False False False False]
[False False False False False]]
[[False False False False False]
[False False False False False]
[False False False False False]]]
barrier
[[[False True False False False]
[False False False False False]
[False False False True False]]
[[False True True True True]
[ True True True True True]
[ True True True True True]]
[[False False False False False]
[ True False True True True]
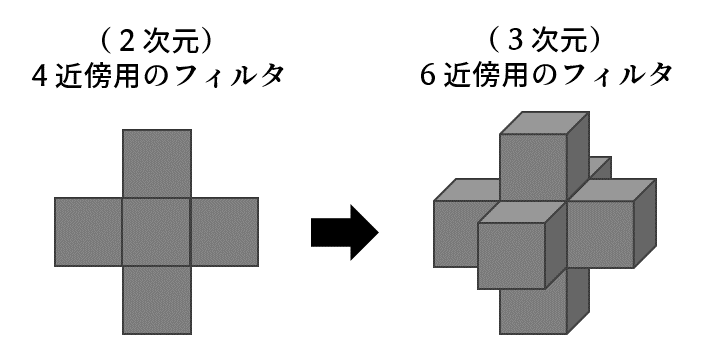
[False False False False False]]]注意が必要なのはプーリング(4近傍でもっとも小さい数を書き込む処理)用のフィルタでしょうか。前回は2次元配列用だったものが、今回は3次元配列用になっています。3次元にも対応できるんですね~(感心)。
*やっぱりこのコードも999ステップ以上には対応していません。
表示関数
グラフを表示する関数も前回と似ていますが、3次元グラフの表示は少し大変ですので、コードは長くなりました。
#########################
# コストの表示関数
#########################
def show(step):
#通れる場所の座標、障害物の座標
x_t, y_t, z_t = np.where(barrier == True)
x_f, y_f, z_f = np.where(barrier == False)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
#通れる場所、障害物の表示
ax.scatter(x_f, y_f, z_f, c='y', s=200) #通れる場所は黄色
ax.scatter(x_t, y_t, z_t, c='k', s=200) #障害物は黒
#スタート、ゴールの記入
ax.text(start[0]+0.1, start[1], start[2], 'S', size = 20, color = 'r')
ax.text(goal[0]+0.1, goal[1], goal[2], 'G', size = 20, color = 'b')
#コストの記入
x, y, z = np.where(cost != 999)
c = cost[x, y, z]
for i in range(len(x)):
ax.text(x[i]-0.1, y[i]+0.1, z[i], c[i], size = 15, color = 'k')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
ax.view_init(25, -75)
#plt.savefig('save/{}.png'.format(step), bbox_inches='tight', pad_inches=0)
plt.show(), plt.close(), print()
#表示
show(0)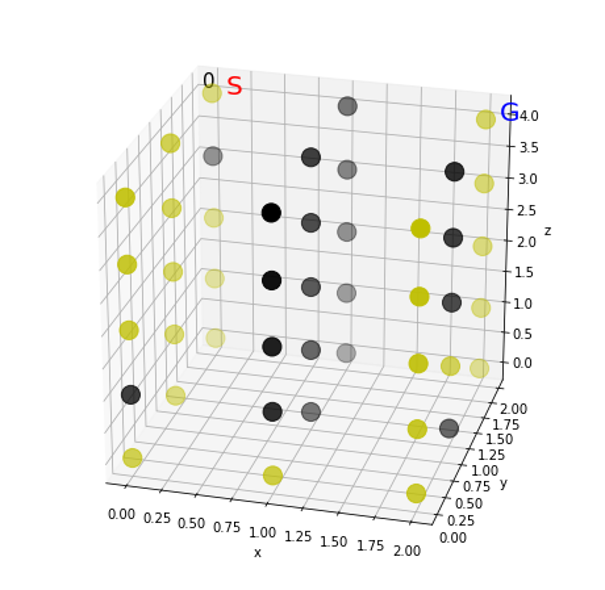
黄色は通れる場所、黒は障害物です。コスト配列のうち999でない数字がグレーで書き込まれます。スタート地点だけが書き込まれていますね。
ネタバレになりますが、最短経路は次のようになるはずです。
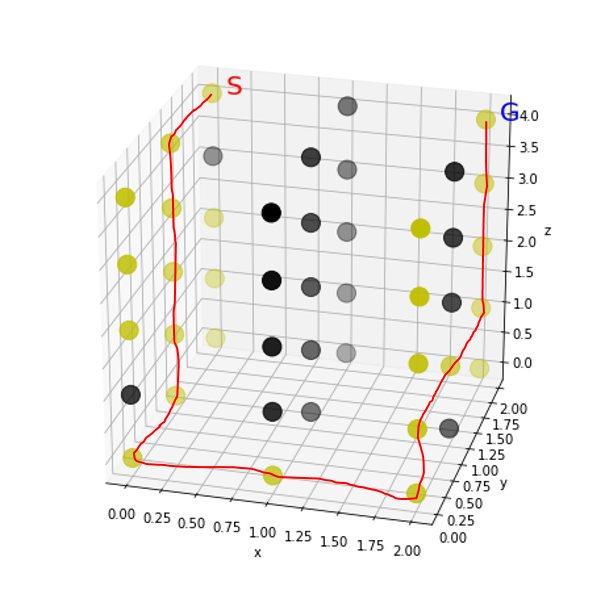
幅優先探索で迷路を探索する
肝心の探索部分は、実はほとんど前回と同じで済みます。配列ごと計算をするPythonの(というかnumpyの?)の強みですね。前回とどこが違うか、間違い探しを楽しみましょう。
#########################
# 幅優先探索
#########################
for i in range(1, 999):
#次に進出するマスのbool
done_next = maximum_filter(done, footprint=g) * ~done
#print('done_next\n{}'.format(done_next))
#次に進出するマスのcost
cost_next = minimum_filter(cost, footprint=g) * done_next
cost_next[done_next] += 1
#print('cost_next\n{}'.format(cost_next))
#costを更新
cost[done_next] = cost_next[done_next]
#ただし障害物のコストは999とする
cost[barrier] = 999
#print('cost\n{}'.format(cost))
#探索終了マスを更新
done[done_next] = done_next[done_next]
#ただし障害物は探索終了としない
done[barrier] = False
#print('done\n{}'.format(done))
#表示
show(i)
#終了判定
if done[goal[0], goal[1], goal[2]] == True:
break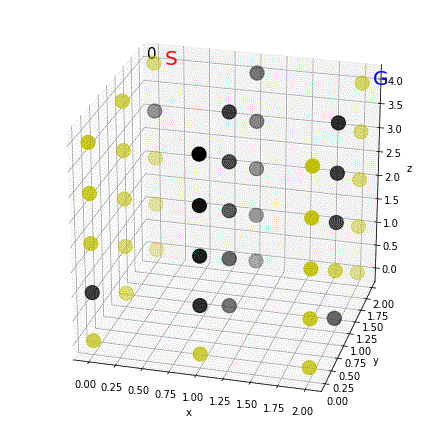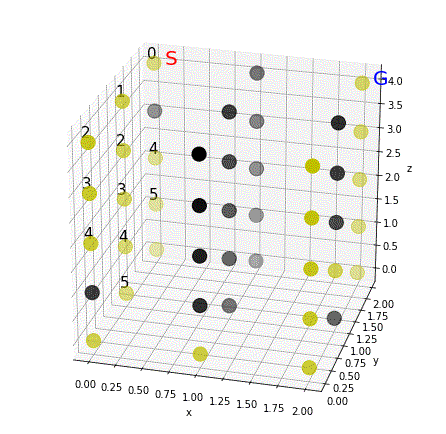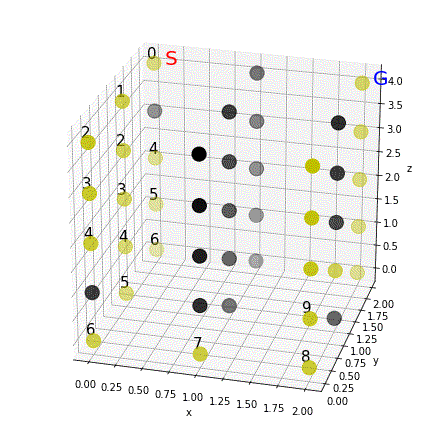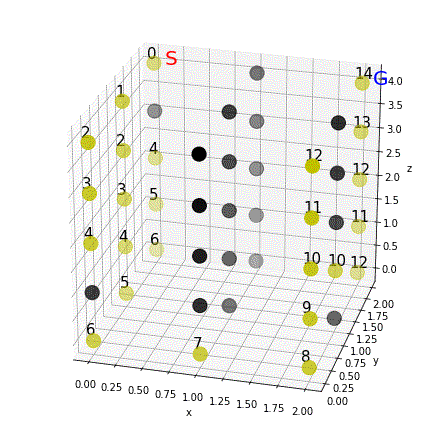
ルートのあぶり出し
※2022/09/20修正
ゴールから逆にたどって、最短ルートをあぶり出します。前回は2次元配列でしたので、4近傍のどの方向から来たかを繰り返しチェックしました。今回は3次元配列なので、6近傍のどの方向から来たかをチェックします。
#########################
# ゴールから逆順でルート計算
#########################
point_now = goal
cost_now = cost[goal[0], goal[1], goal[2]]
route = [goal]
print('route\n{}'.format(route))
while cost_now > 0:
#x-から来た場合
if 0 <= point_now[0] - 1 and cost[point_now[0] - 1, point_now[1], point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0] - 1, point_now[1], point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
#x+から来た場合
if point_now[0] + 1 < h and cost[point_now[0] + 1, point_now[1], point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0] + 1, point_now[1], point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
#y-から来た場合
if 0 <= point_now[1] - 1 and cost[point_now[0], point_now[1] - 1, point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1] - 1, point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
#y+から来た場合
if point_now[1] + 1 < w and cost[point_now[0], point_now[1] + 1, point_now[2]] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1] + 1, point_now[2])
cost_now = cost_now - 1
#記録
route.append(point_now)
#z-から来た場合
if 0 <= point_now[2] - 1 and cost[point_now[0], point_now[1], point_now[2] - 1] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1], point_now[2] - 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
#z+から来た場合
if point_now[2] + 1 < l and cost[point_now[0], point_now[1], point_now[2] + 1] == cost_now - 1:
#更新
point_now = (point_now[0], point_now[1], point_now[2] + 1)
cost_now = cost_now - 1
#記録
route.append(point_now)
#ルートを逆順にする
route = route[::-1]
print('route\n{}'.format(route))route
[(2, 2, 4)]
route
[(0, 2, 4), (0, 1, 4), (0, 1, 3), (0, 1, 2), (0, 1, 1), (0, 1, 0), (0, 0, 0), (1, 0, 0), (2, 0, 0), (2, 0, 1), (2, 1, 1), (2, 2, 1), (2, 2, 2), (2, 2, 3), (2, 2, 4)]逆順にたどる前、route配列にはゴールの位置が記録されています。ここからコストが一つずつ小さくなる方向に進みながらroute配列に座標を加えていきます。コストが0のところまで来たら終了です。route配列を逆順にひっくり返したら完成です。
※チェックする座標の添字は、x方向は0以上h未満、y方向は0以上w未満、z方向は0以上l未満の範囲であることに注意しましょう。
一応、ルートを可視化する関数を置いておきますね。
#########################
# ルートの表示関数
#########################
def show_route(route):
#通れる場所の座標、障害物の座標
x_t, y_t, z_t = np.where(barrier == True)
x_f, y_f, z_f = np.where(barrier == False)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
#通れる場所、障害物の表示
ax.scatter(x_f, y_f, z_f, c='y', s=200) #通れる場所は黄色
ax.scatter(x_t, y_t, z_t, c='k', s=200) #障害物は黒
#スタート、ゴールの記入
ax.text(start[0]+0.1, start[1], start[2], 'S', size = 20, color = 'r')
ax.text(goal[0]+0.1, goal[1], goal[2], 'G', size = 20, color = 'b')
#コストの記入
for i in range(1, len(route)):
ax.plot([route[i - 1][0], route[i][0]], [route[i - 1][1], route[i][1]], [route[i - 1][2], route[i][2]], c='r')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
ax.view_init(25, -75)
#plt.savefig('save/{}.png'.format(step), bbox_inches='tight', pad_inches=0)
plt.show(); plt.close()
#表示
show_route(route)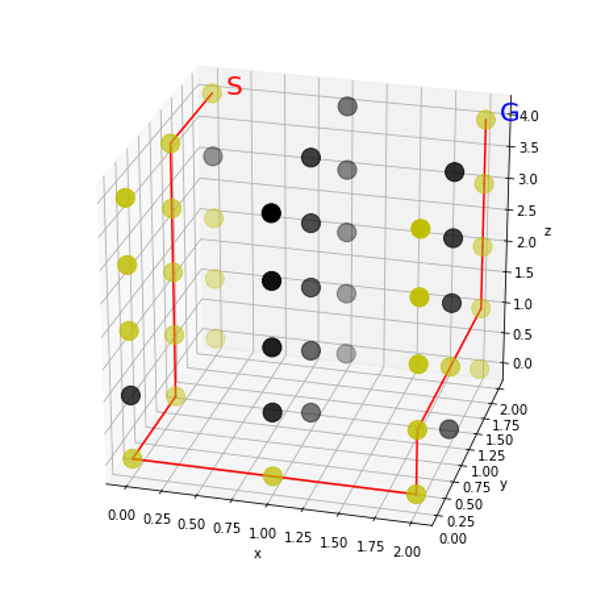
ねらい通りのルートがあぶり出されました!
大きな迷路で
#########################
# 迷路
#########################
maze = [['s-#-####------##-##--##-#######----##---',
'##---#-#-###----##-#--#-#-#-#-#--####-#-',
'-#-#--#-----#---##-#-###-#-----#--------'],
['----#-#--#-----###-#---#-#-----#-----#--',
'##-##----###-#---#######-##-###--#####--',
'##-#------#-----------------#-#---##-#--'],
['-----##-#-----###--###--##--#---#--#-#-#',
'####--#----#-----##------##--#--####-#--',
'#-##--#---##----#-#-###--#---####---#-#g']] 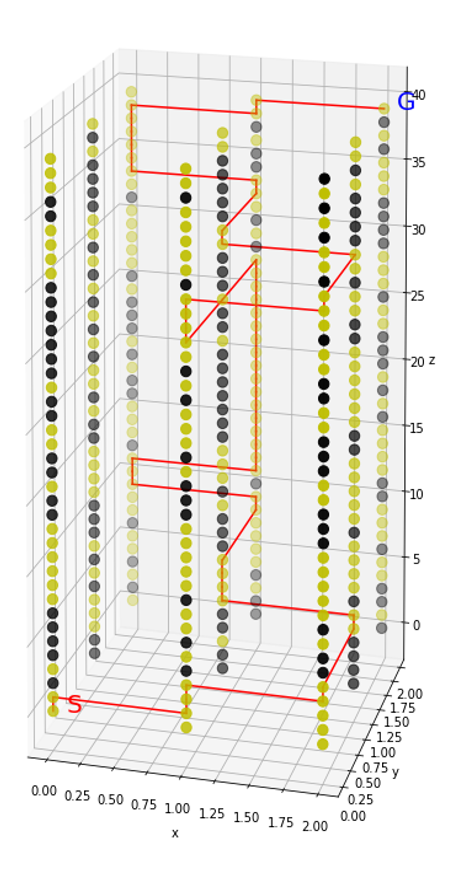
素晴らしい出来栄えです。