やること
「日本一わかりやすい」は流石に盛りました。タイトル詐欺です。
最適化をやっているとどうしても「NP完全」を理解しなければなりません。しかし、NP完全を検索しても「NP困難のうちNPであるもの」といった定義ばかりでさっぱりです。
今日は日本一わかりやすいNP完全の説明を目指します。一度諦めた方もぜひ挑戦してみてください。
計算量オーダーとは
ビネクラ中学校1年A組には男女合わせて40人います。人数は転校生が来て変わるかもしれないので N としておきます(N=40)。次の問題の答えを求めるにはどれくらいの計算量が必要かを考えます。
(1)田中は男の子ですか?
Pythonですみませんが、プログラミング的には
print(sex['田中'] == 'male')のような1行で、True/False の答えがわかります。Nがどんなに増えてもこの1行で済みますので、計算量オーダーは O(1) (オーダーイチ)と呼びます。
(2)転校生の小林さんが来ました。小林さんを背の順に加えたとき、男の子の後ろですか?
ただし40人の背の順は完成しており、身長を測る機械はないものとします。担任の先生はこう考えました。
列の真ん中の人と背比べをして、小林さんが低ければ低い側のグループ、高ければ高い側のグループに入れる。これを繰り返せば小林さんの位置がわかる!
このような探索方法を二分探索と呼びます。二分探索は半分にして半分にして…というアルゴリズムなので、Nが2の何乗なのかが重要になります。計算量オーダーは、 O(logN) であることが知られています。この場合のlogの底は2ですが、底は何であっても O(logN) と表記します。N=40 であれば最大で 6回 のチェックが必要です。
(3)クラスに伊藤はいますか?
プログラミング的には
for i in range(40):
if name[i] == '伊藤':
print('います')このような1重for文で答えがわかります。N回だけチェックを行うため、計算量オーダーは O(N) (オーダーエヌ)と呼びます。N=40 であれば40回のチェックとなります。
(4)背の順に並んでください。男の子が5人連続する部分はありますか?
ただし40人の背の順は完成しておらず、身長を測る機械はないものとします。担任の先生はこう考えました。
2人組で背比べをして、低かった人を左に置く。2人組を2つ合体して4人組となり、低かった人同士で順々に背比べをしてまた低い順に並ぶ。これを繰り返せば背の順が完成する!
このような並び替え方法(=ソート方法)をマージソートと呼びます。マージソートの計算量は O(NlogN) (オーダーエヌログエヌ)であることが知られています。
厳密に言えば背の順が完成した後に、1重for文で男の子が5人連続する部分があるかどうかを調べなければなりませんが、この作業にかかる O(N) は O(NlogN) よりも小さいため無視します。よって計算量オーダーは O(NlogN) です。N=40 であればおよそ210回のチェックが必要です。
(5)クラスに誕生日が同じペアはいますか?
プログラミング的には
for i in range(40):
for j in range(i+1, 40):
if birthday[i] == birthday[j]:
print('います')のような2重for文で答えがわかります。チェック回数は NC2=N(N-1)/2 であり、最高次数が N2 であることから、計算量オーダーは O(N2) となります。N=40 であれば N(N-1)/2=780回のチェックが必要です。
(6)2年生のクラス分けを行います。1年A組のすべての友達関係が崩れないクラス分けのパターンはありますか?
ただし1年A組の40人はそれぞれ2年A・B組にランダムで振り分けられるとします。クラス分けは無慈悲ですので、違うクラスになってしまったらもう友達ではありません。
プログラミング的には、あらゆるクラス分けのパターンを試してみて、条件を満たすパターンがあるかを探さなければなりません。40人のクラス分けのパターンは全部で 240 通りあるため、計算量オーダーは O(2N) となります。240 = 約1兆回のチェックが必要です。
(7)家庭訪問のルートを決めます。ガソリンを一度も給油しないで済むルートはありますか?
ただし家庭訪問は1日で40人分強行します。最近は家庭訪問ってあるのでしょうか?
プログラミング的には、あらゆるルートを列挙してみて、条件を満たすルートがあるかを探さなければなりません。40人の家を回るルートは全部で 40! 通りあるため、計算量オーダーは O(N!) となります。40! = 約1極(ゼロが48個)回のチェックが必要です。
計算量オーダーまとめ
以上の問題と計算量オーダーをまとめます。
| 問題の略称 | 計算量オーダー | N=40のときのチェック回数 |
| (1)田中の性別 | O(1) | 1 |
| (2)小林の位置 | O(logN) | 6 |
| (3)伊藤の存在 | O(N) | 40 |
| (4)背の順の奇跡 | O(NlogN) | 約210 |
| (5)誕生日が一緒 | O(N2) | 約780 |
| (6)クラス分けと友情 | O(2N) | 約1兆 |
| (7)家庭訪問と給油 | O(N!) | 約1極(ゼロが48個) |
各問題は「1つでもありますか?」と聞いているので、実際には1例を見つけた次点で終了し、チェック回数が表記より少なくて済むことがあります。しかし計算量オーダーの世界では最悪のケースを想定するため、「全パターンをチェックして一番最後に見つけた」の場合で考えます。
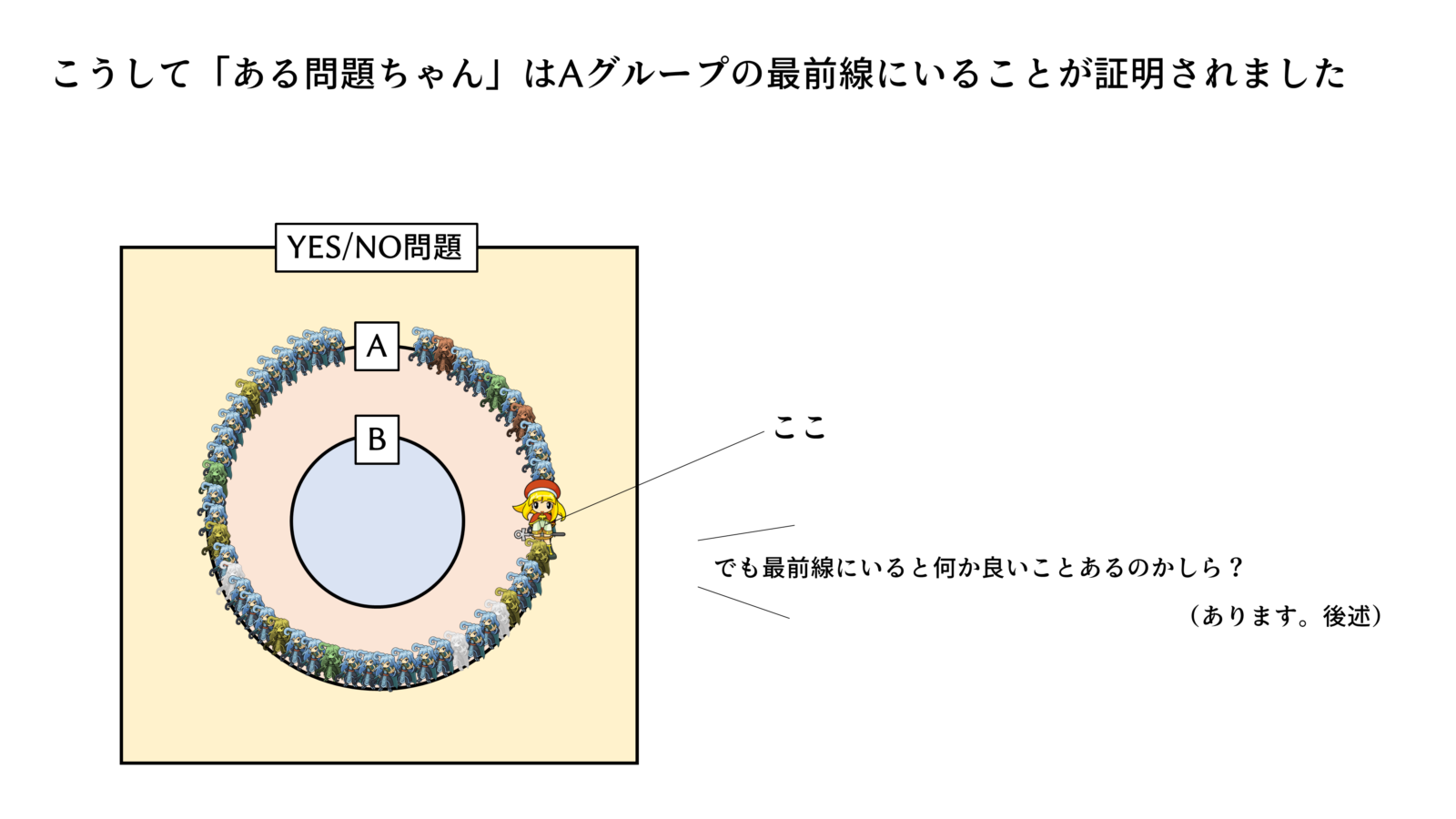
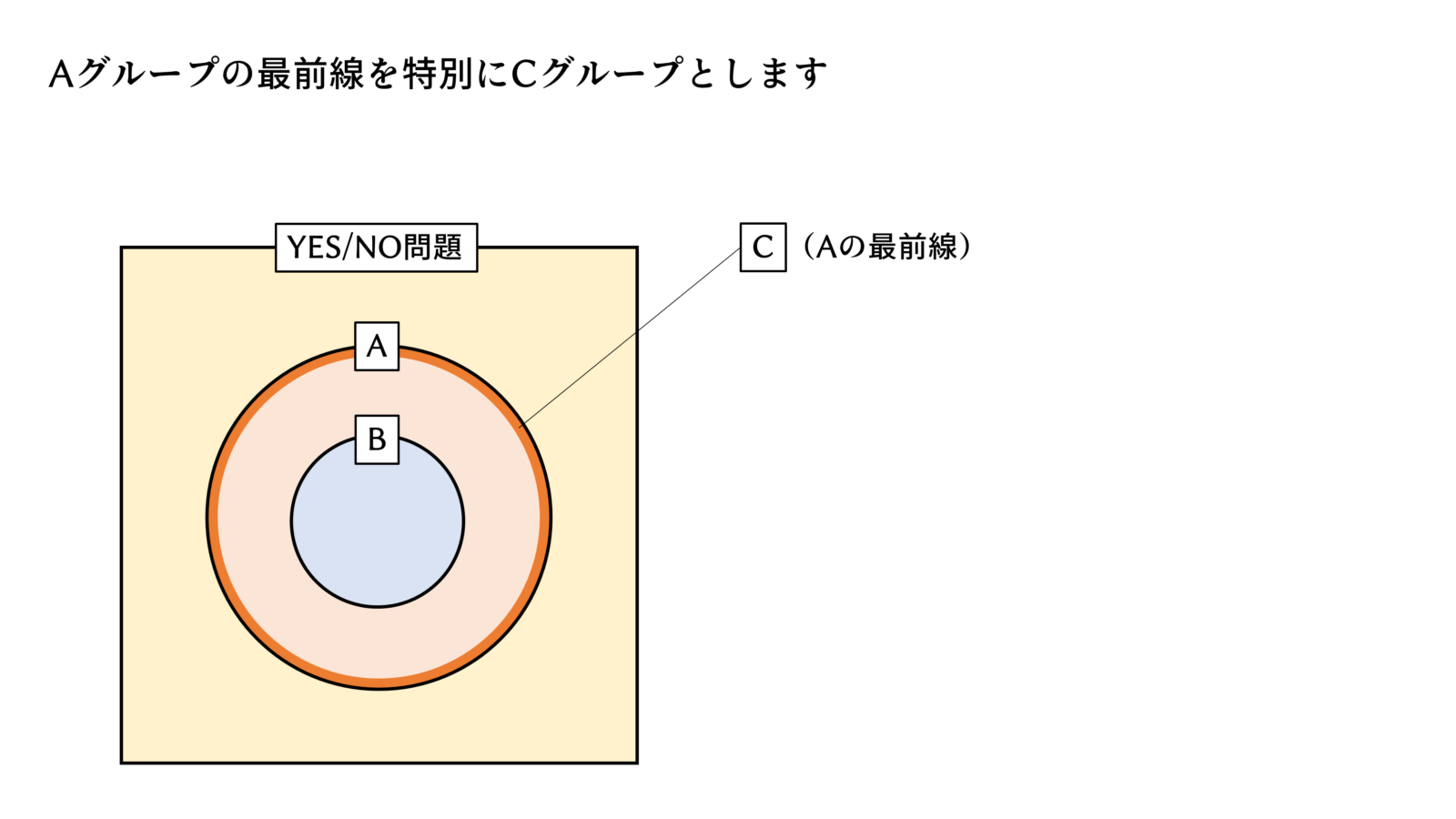
NP完全とは
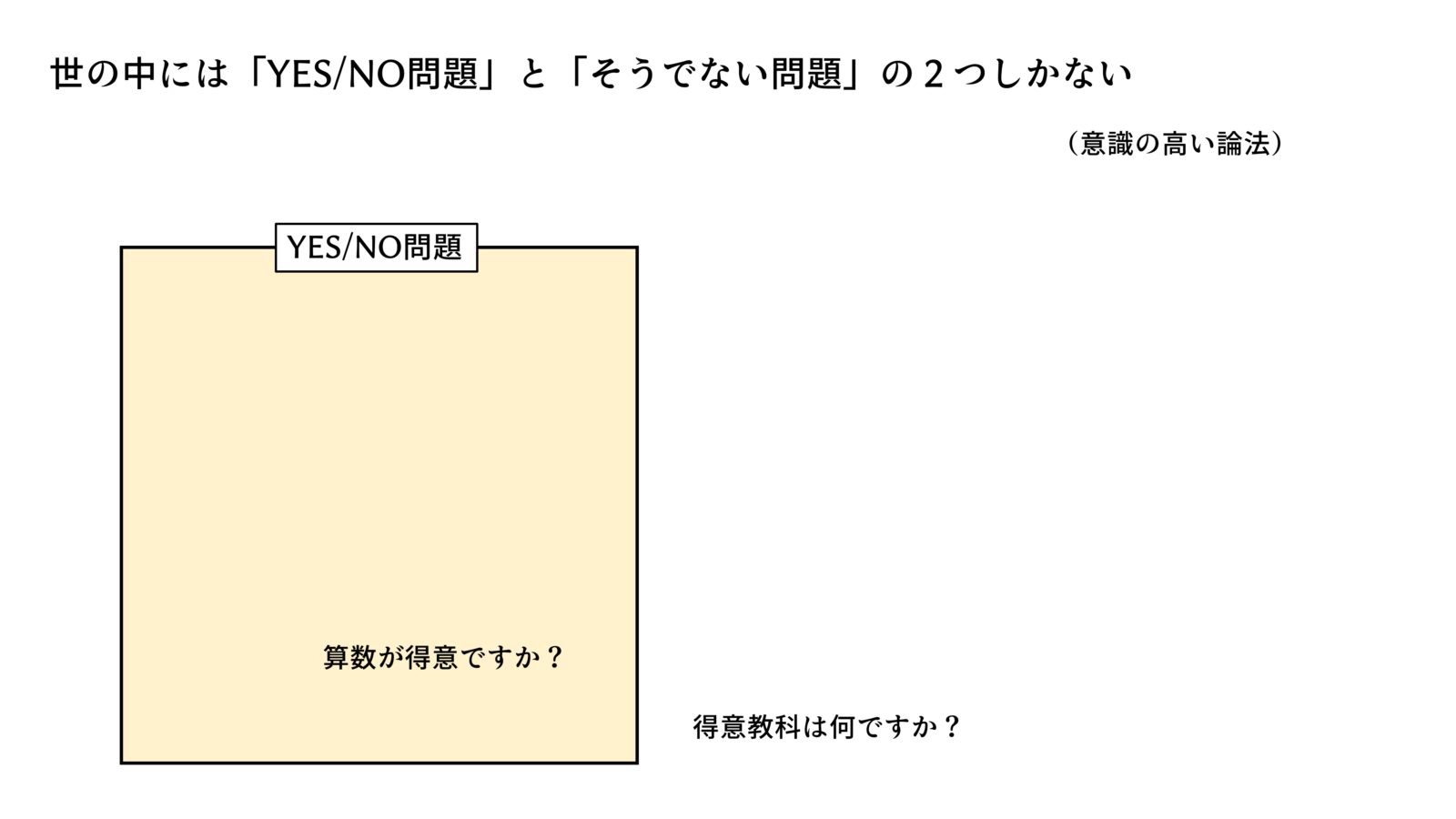
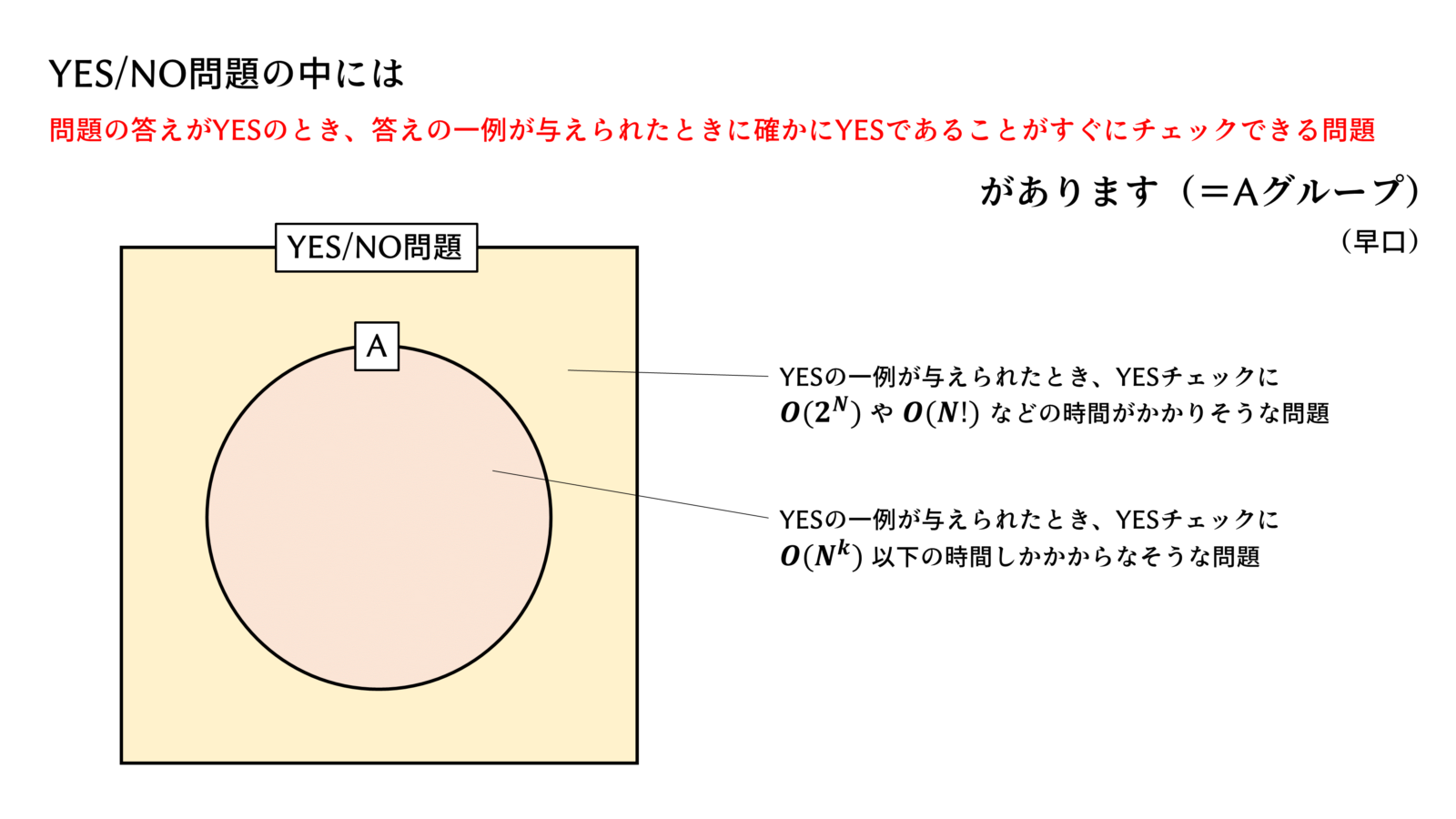
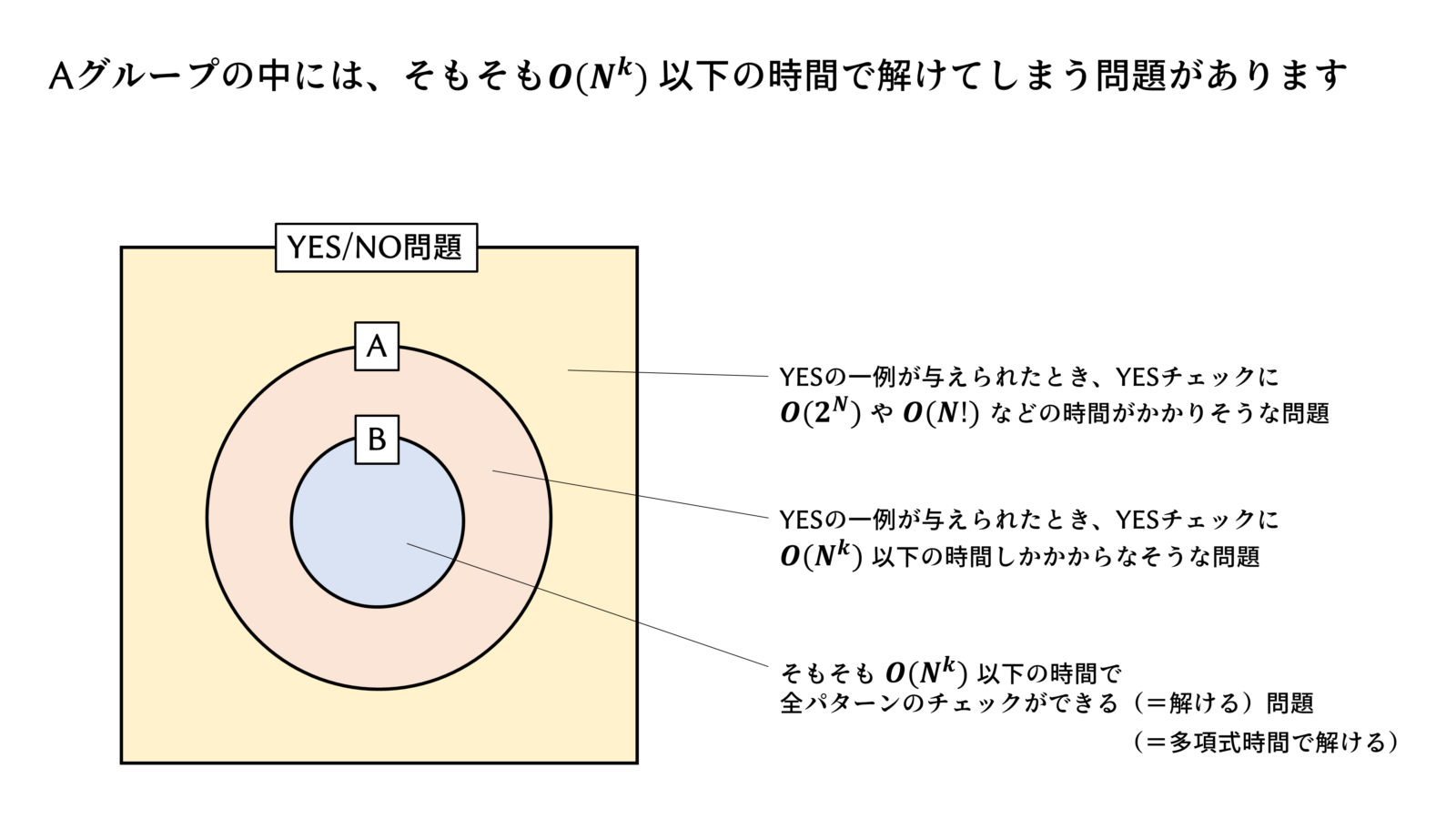
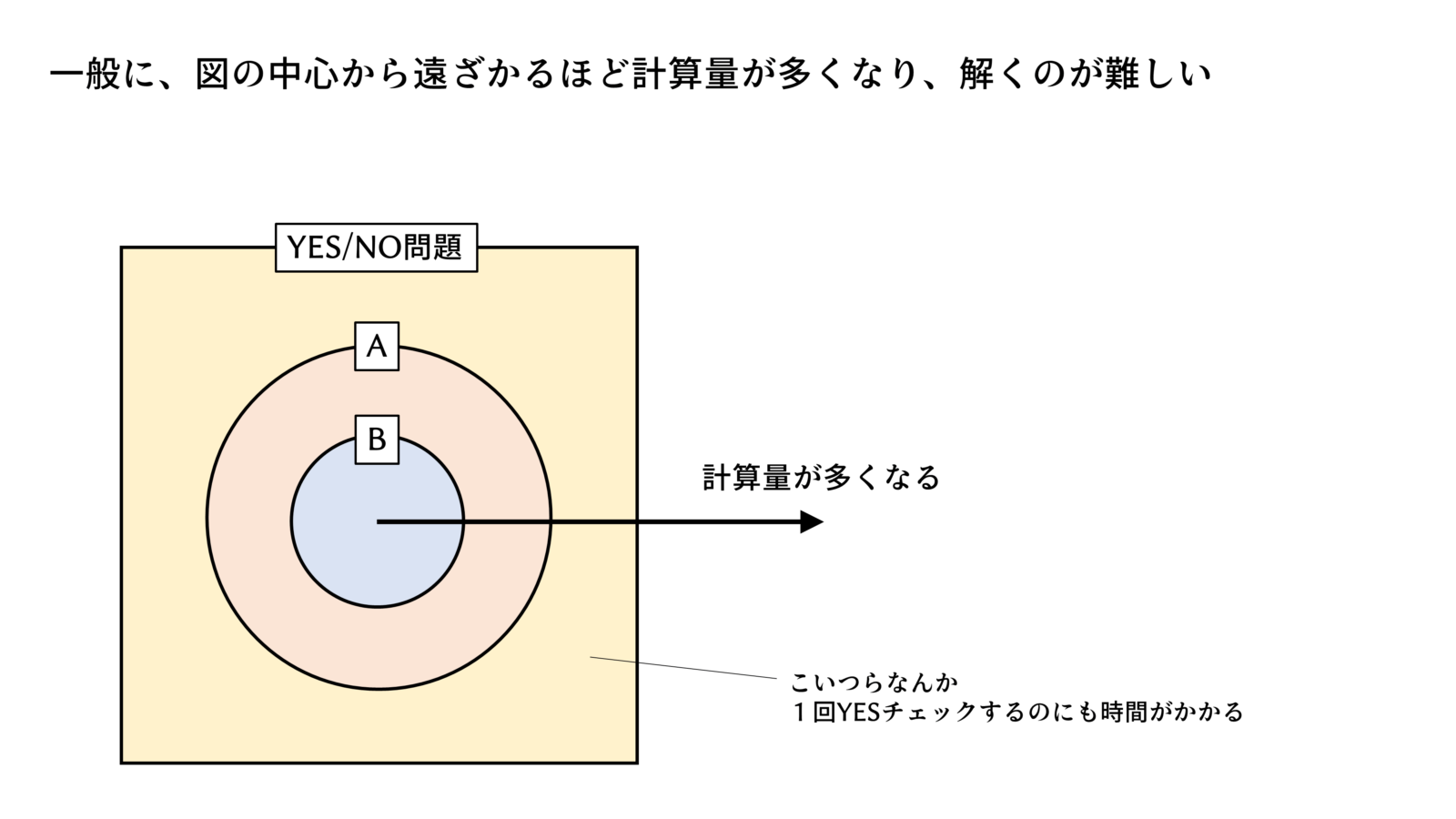
スライドで説明します。
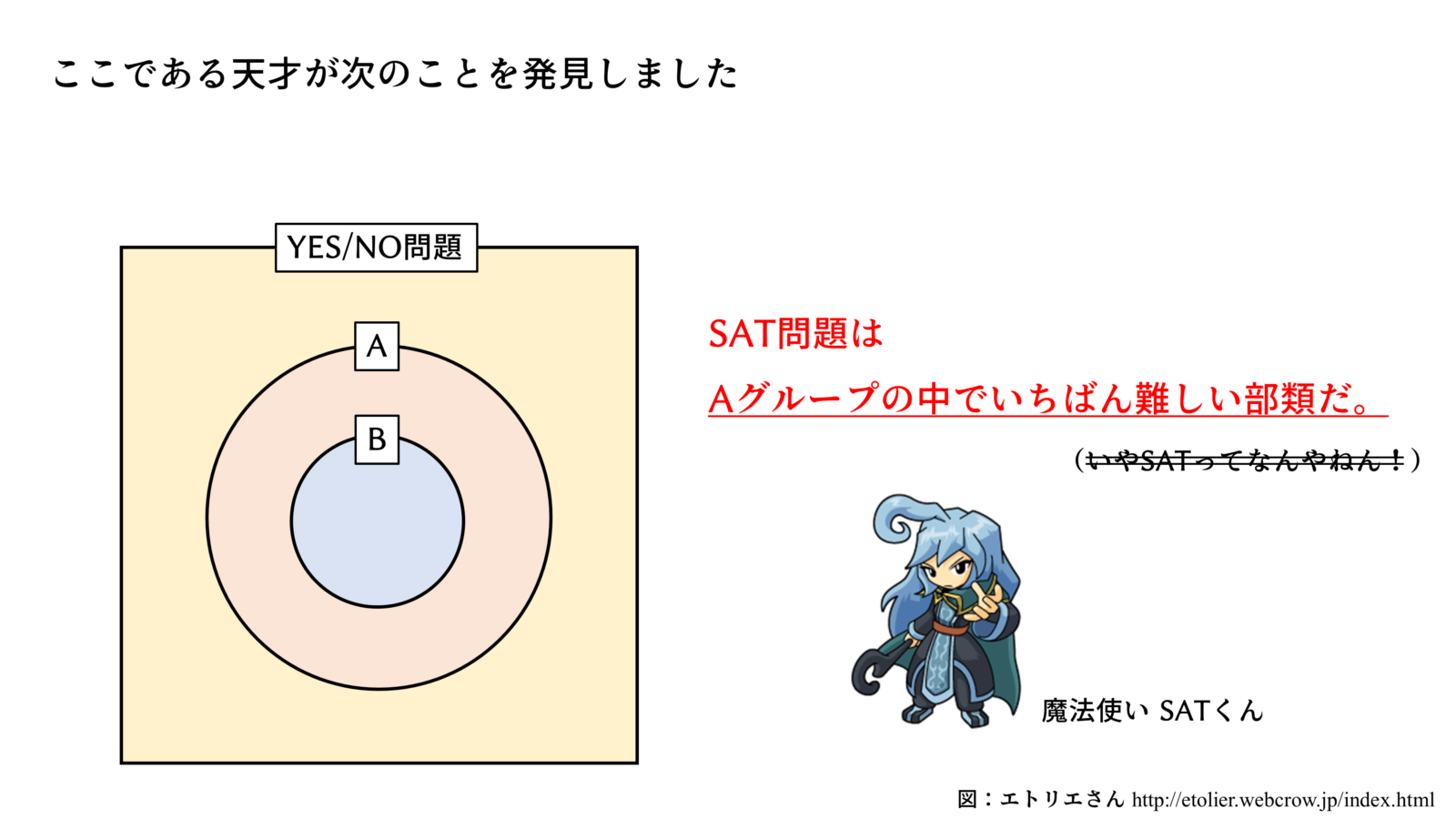
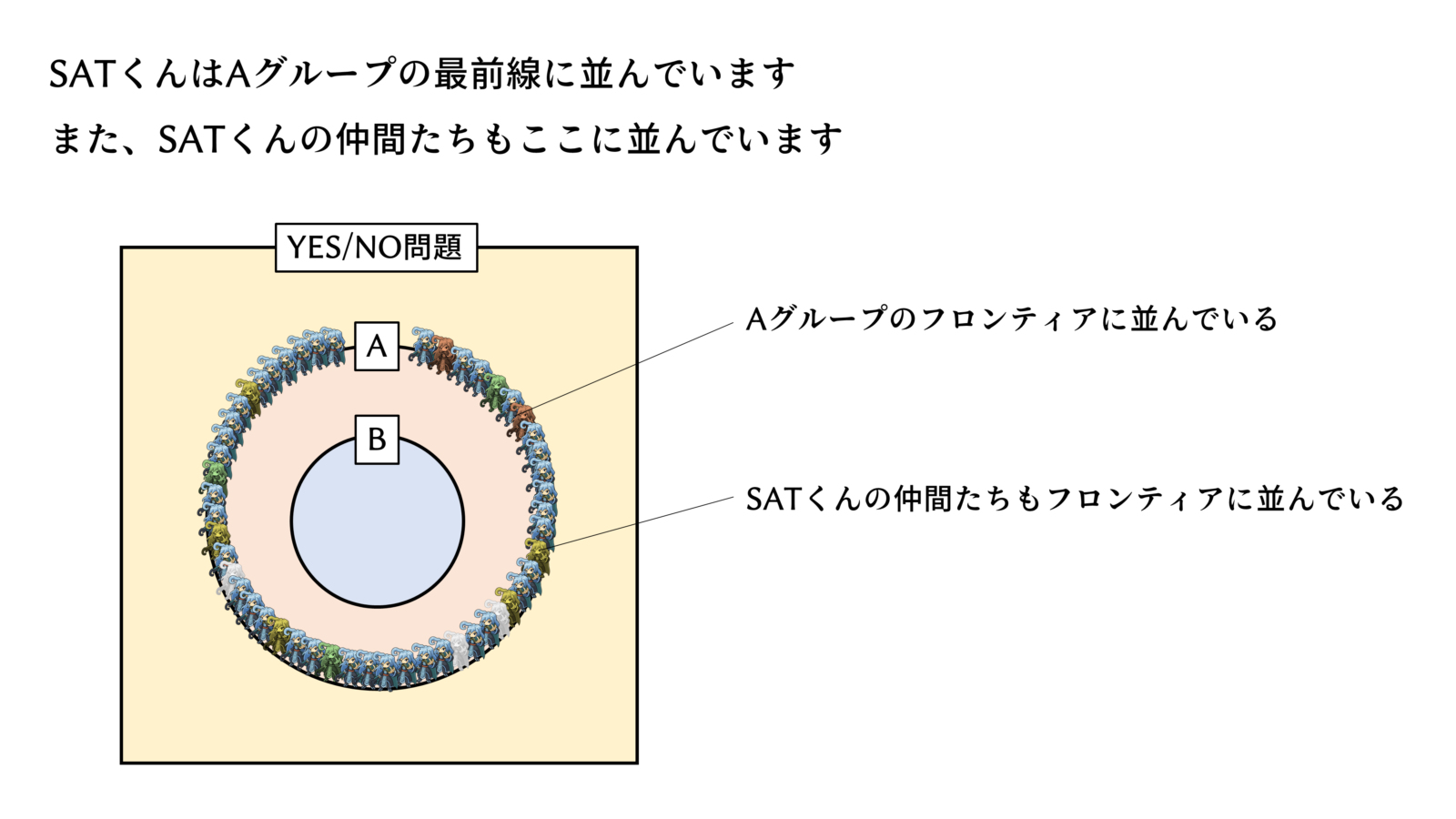
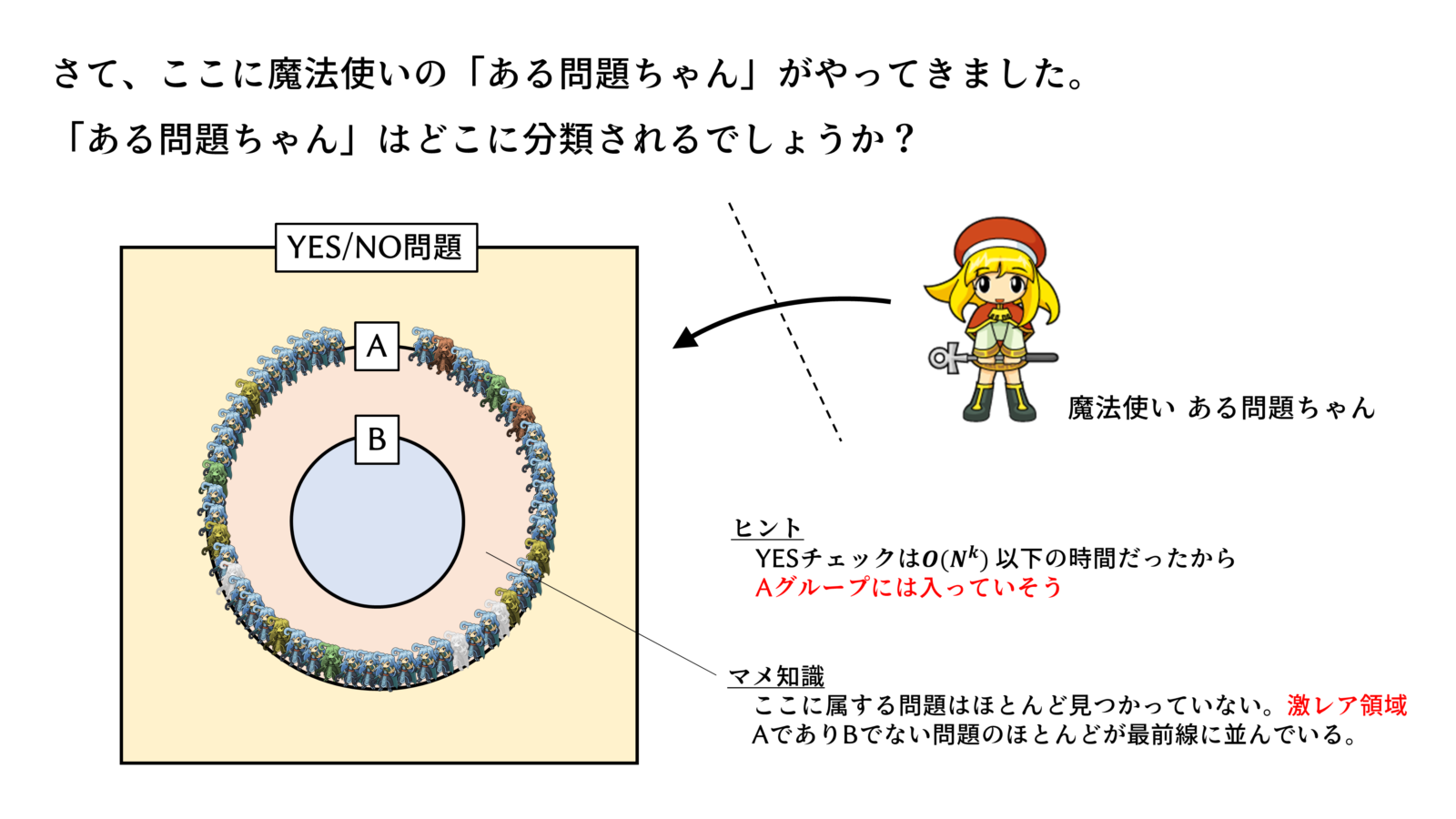
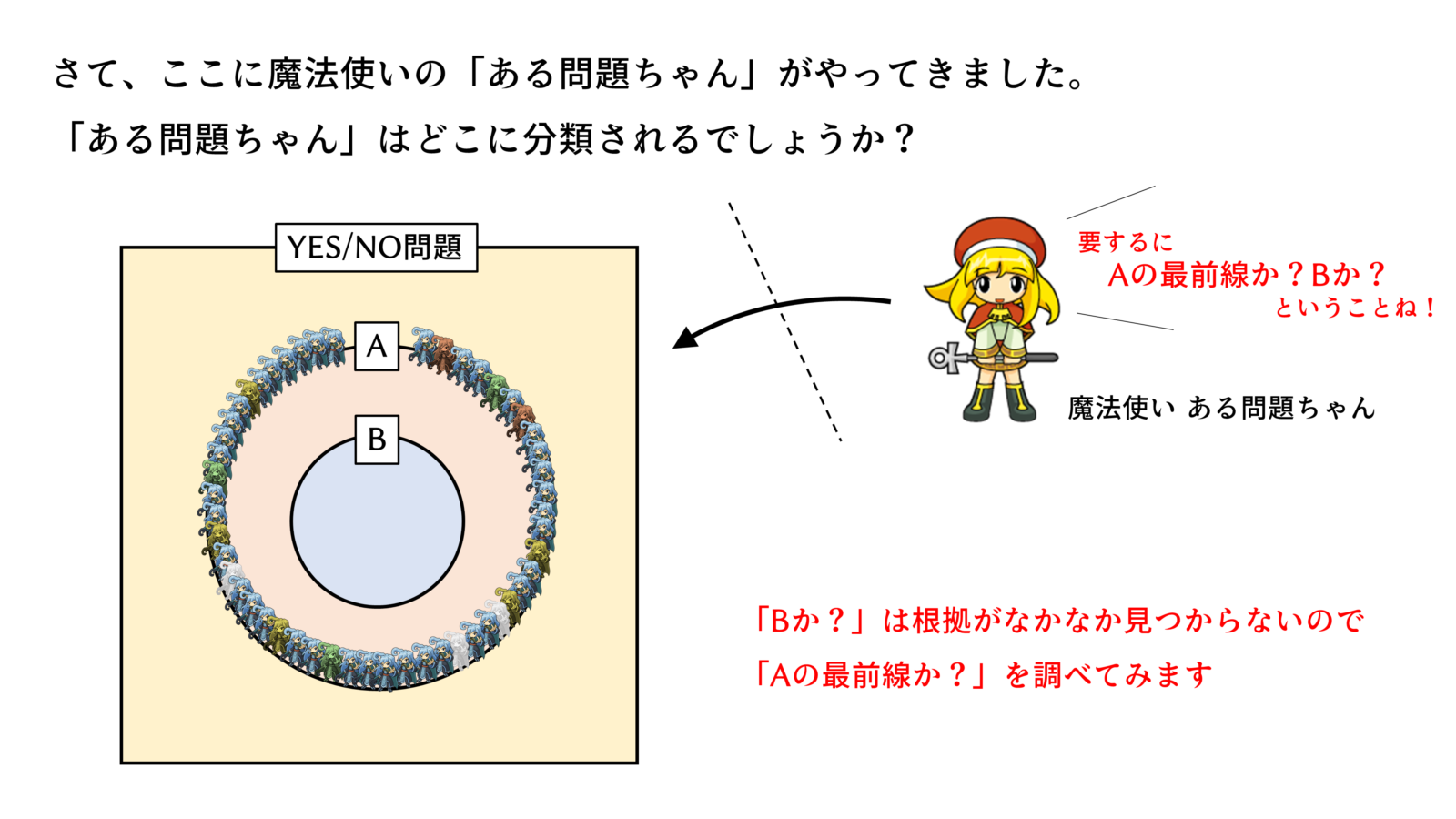
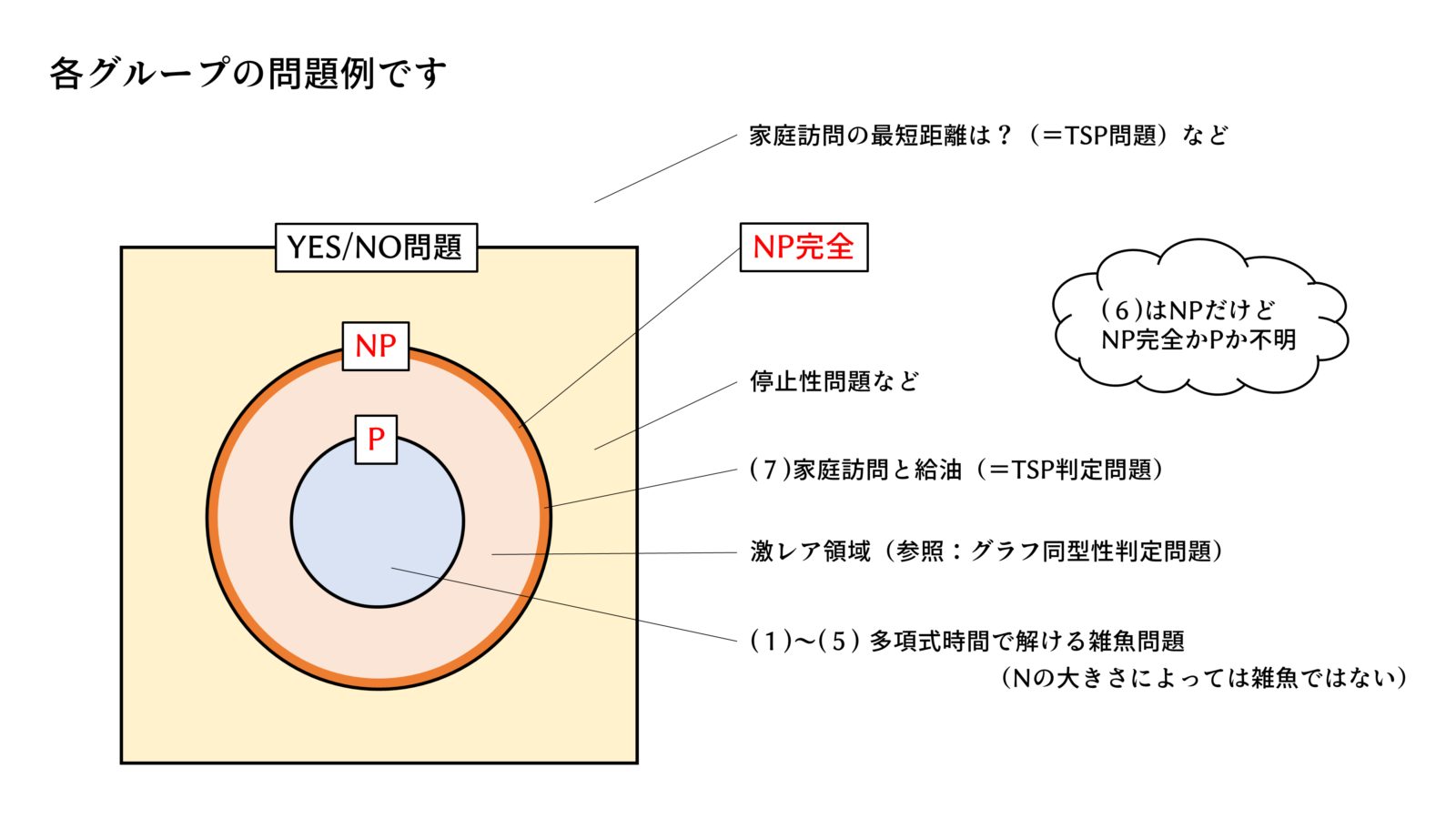
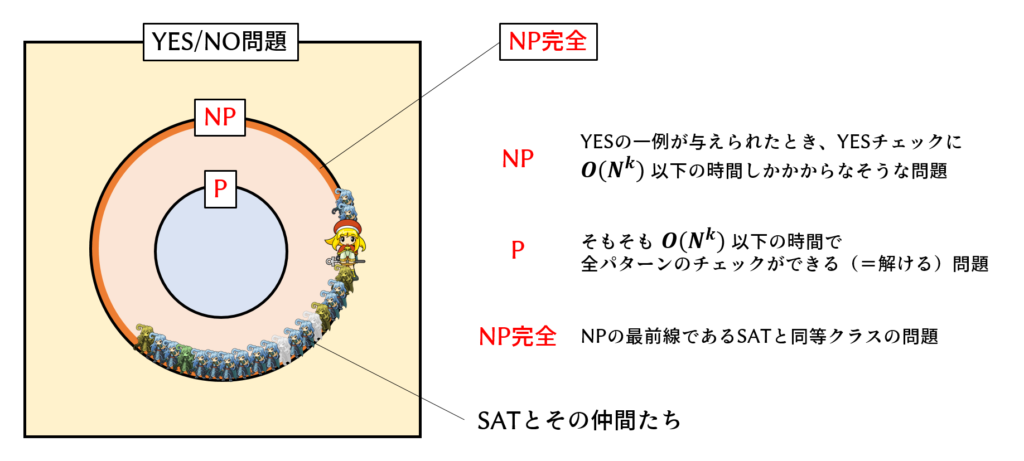
これが本日のポイントです。
補足
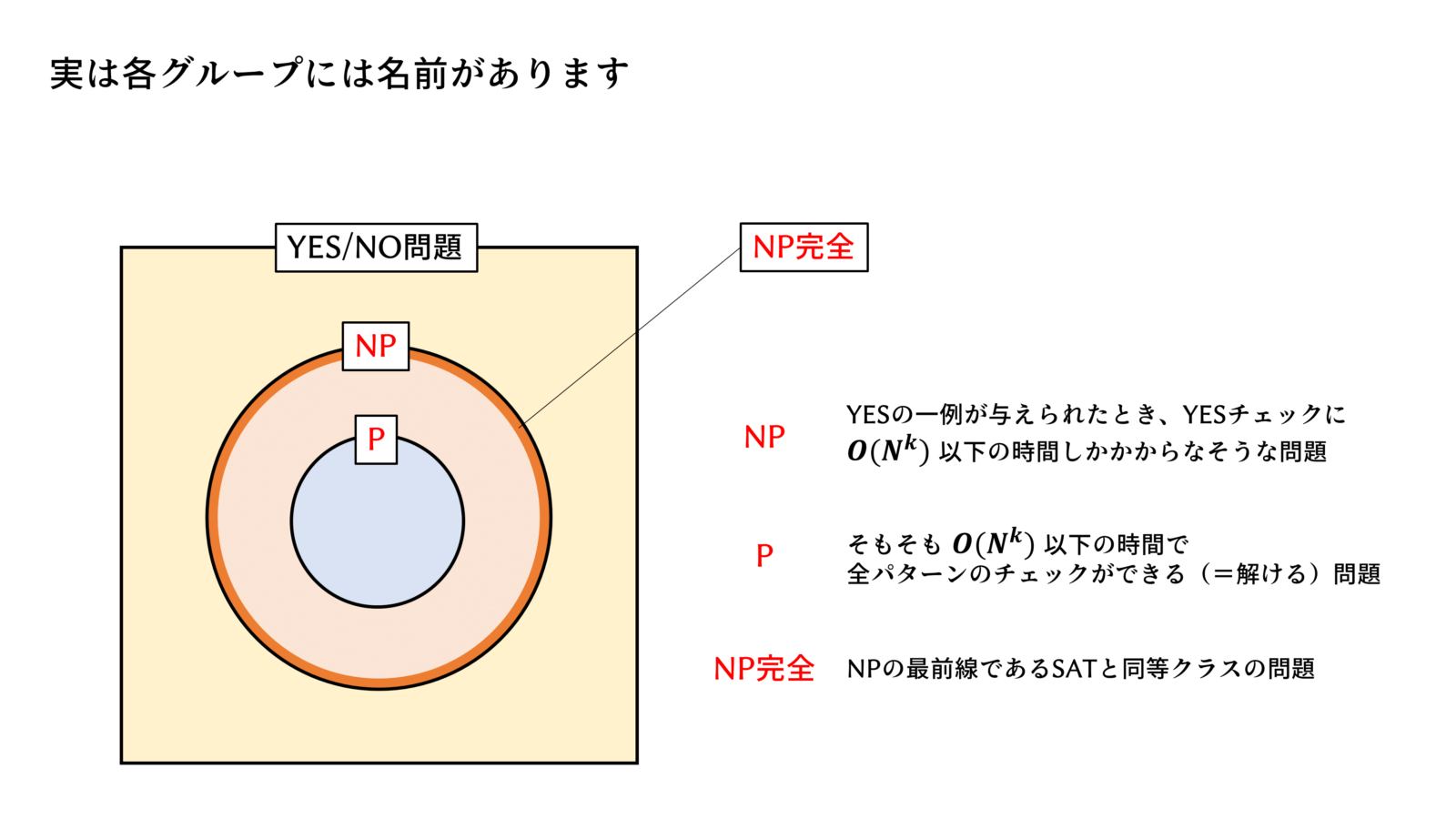
P は Polynomial(多項式時間で解けるよ)、NP は Non-deterministic Polynomial(要するにYESチェックは多項式時間でできるよ)、NP完全(NP complete)の”完全”については考えないでください。
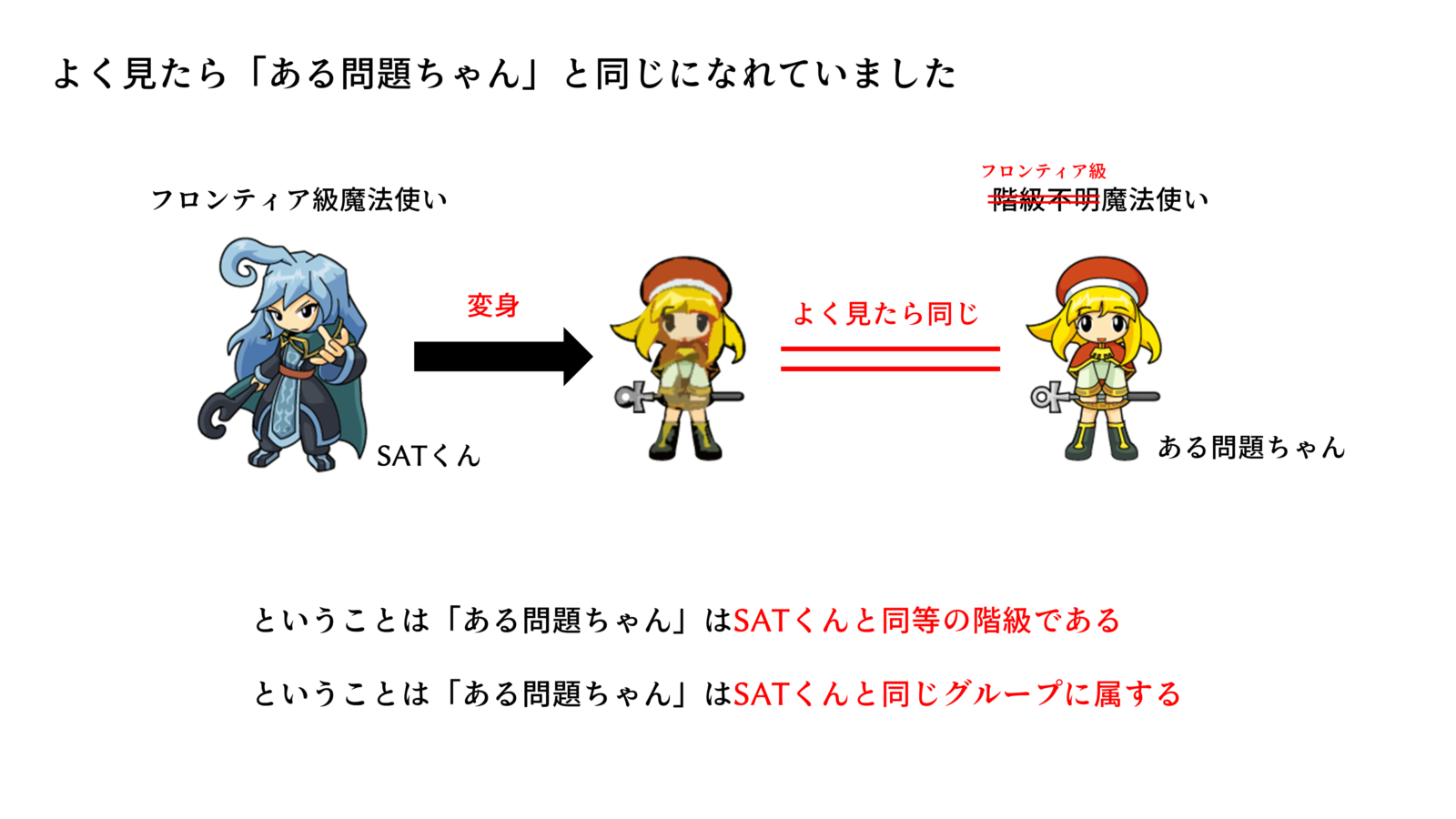
SAT(充足可能性問題)がNP完全であることは1971年にStephen A. Cookさんが証明しました。
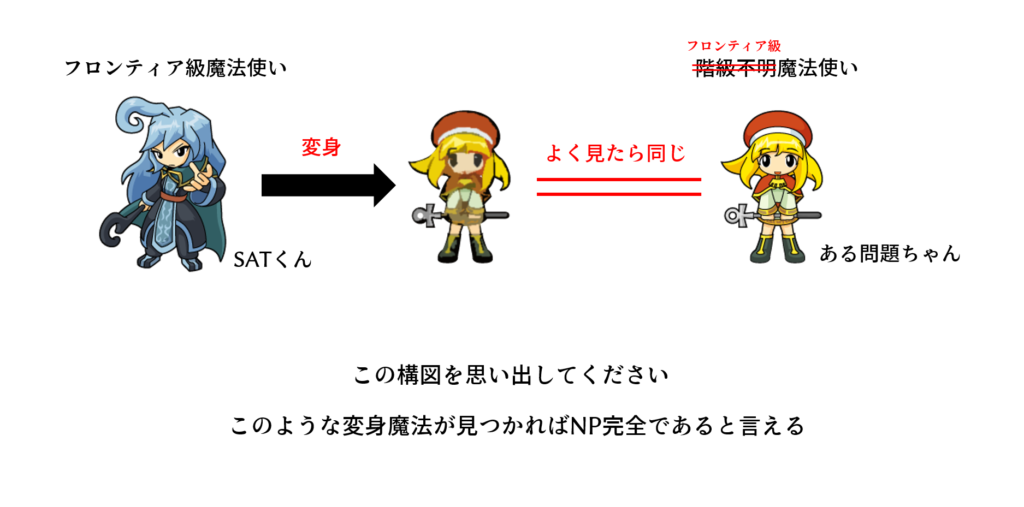
NP完全であると何が嬉しいのか?
では、世の中の人々はなぜ「ある問題がNP完全であるか?」を血眼になって調べているのでしょうか?
答えは、NP完全であれば解くのをサボれるからです。
ある問題がNPに含まれるかどうかを判断するのは簡単です。なぜなら、YESチェックが多項式時間で済むかどうかを調べればよいからです。しかし、Pに含まれるかどうかを判断するのは極めて困難です。なぜなら、多項式時間で解けるアルゴリズムが現状で見つかっていなかったとしても、神のみぞ知る「多項式時間で解けるアルゴリズム」が存在するかもしれないからです。そんなものを100万年かけて探し続けるのは精神衛生上たいへん辛いです。
そこで、NP完全であることをがんばって示します。これが示されれば、すなわち多項式時間で解けない(※)ということです。多項式時間で解けないということは、神のみぞ知るアルゴリズムを探す作業をさっさと諦めて、遺伝的アルゴリズム(GA)等のメタヒューリスティックな手法で近似解を求める作戦に切り替えることができます。心が晴れやかになります。
※NP完全なのに多項式時間で解けるアルゴリズムが見つかったとしたらとんでもないことが起きます。上の図で、PとNPは一致しないと一般に考えられています。NP完全なのに多項式時間で解けるアルゴリズムが見つかった場合、すべてのNP完全問題(SATとその仲間たち)が芋づる式にPに落ち込み、P=NPということになります。P=NPの証明は懸賞金付きの問題となっており、根拠を見つけたら世界中の数学者が泡を吹いて倒れます。
テント・アンド・ツリーパズルがNP完全であるかどうか
20-2ではテント・アンド・ツリーパズルをGAで解きました。
21-4ではテント・アンド・ツリーパズルを量子アニーリングで解きました。
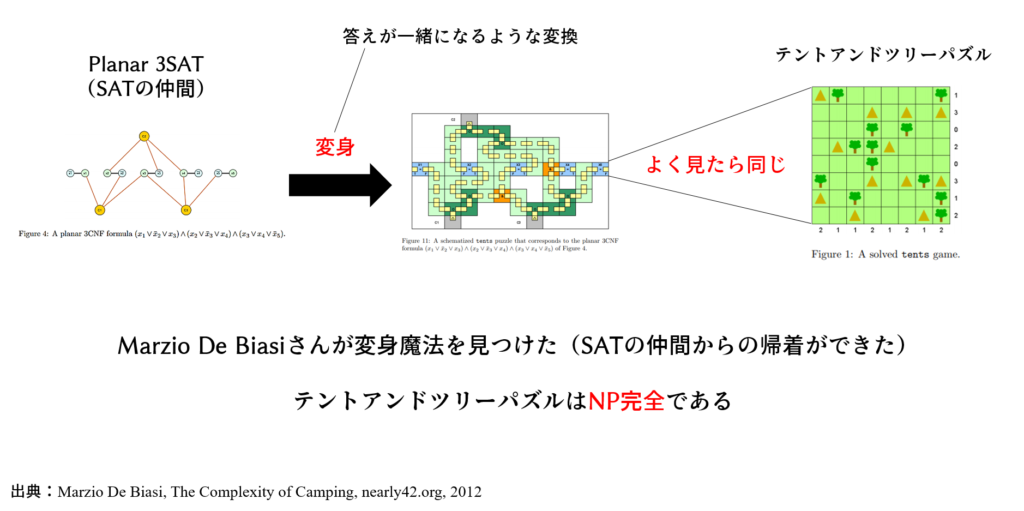
これがNP完全であるかどうか、証明した人がいます。
テント・アンド・ツリーパズルはNP完全問題でした。ということは、多項式時間で厳密解を得るアルゴリズムを探すことはP=NP証明に挑戦することと同義です。これは諦めても仕方がないということで、GAで近似解を得るのが合理的であるというお墨付きが得られるわけです。やっぱりGAは最高だぜ!(宗教)
この他に、ぷよぷよやテトリスもNP完全であることが証明されています。
遺伝的アルゴリズム(GA)はvcoptにおまかせ
vcoptは無料かつ商用利用可能なPythonパッケージです。(宣伝)
編集後記
理解のポイントは「NP困難の説明を捨てる」でした。NP完全とは何か?の説明にNP困難は不要だったのです。人類が先入観に打ち勝った瞬間です。間違いがあればSlackで教えていただけますと幸いです。