やること
「最長しりとり問題」であるポケモンしりとりは真面目な研究テーマです。調べてみると、しりとりの細かなルールは違うものの、285/719匹、あるいは線形計画法で387/802匹といった記録が見つかりました。そこで、vcoptを使ってポケモンしりとりに挑戦してみましょう。
参考文献

実行環境
WinPython3.6をおすすめしています。
vcoptの使い方についてはチュートリアルをご参照ください。
vcoptの仕様については最新の仕様書をご参照ください。本記事執筆時とは仕様が異なる場合があります。
ポケモンのデータベース
全ポケモンのデータベースはこちらを使わせていただきました。
少しだけデータの整形を行います。
- メガとアローラは除外する
- フォルム名は取り除く(デオキシスN→デオキシス、ニャオニクス♂→ニャオニクス、ジガルデ10%→ジガルデ)
- 記号は読み方に変換する(ニドラン♂→ニドランオス、ポリゴンZ→ポリゴンゼット)
整形後のcsvをこちらに置いておきます。(著作権は上記リンク主にありますのでご注意を)
また、次の処理は後ほどプログラム中で行います。
- 語尾の小さい字は大きくする(ピジョット→ピジヨツト)
- 語尾の長音は削除する(バタフリー→バタフリ)
- 効率化のために語尾が「ん」のポケモンは除外
import
まず、今回使うパッケージをインポートします。
import copy
import numpy as np
import matplotlib.pyplot as plt
from vcopt import vcopt全ポケモン名の読み込み
上の「pokemon_status_2.csv」の全行、2列目を読み込みます。
#============================
#全ポケモンデータの読み込み
#============================
#ファイル名
file = open('pokemon_status_2.csv', 'r')
#
data = []
#1行目はラベルなのでカラ読み
file.readline()
#2行目以降のポケモン名だけを読み込む
while 1:
tmp = file.readline().split(',')
if len(tmp) > 1:
data.append(tmp[1])
else:
break
file.close()
#コピーしておく
data_save = copy.deepcopy(data)
print('ポケモンの数:{}'.format(len(data)))
print('最初の4匹:{}'.format(data[:4]))ポケモンの数:802
最初の4匹:['フシギダネ', 'フシギソウ', 'フシギバナ', 'ヒトカゲ']メガとアローラを除いたポケモン数は802匹でした。
データの整形
以下の整形を行います。
- 語尾の小さい字は大きくする(ピジョット→ピジヨツト)
- 語尾の長音は削除する(バタフリー→バタフリ)
- 効率化のために語尾が「ん」のポケモンは除外
#============================
#データの整形
#============================
#配列の要素を削除するときは逆順で処理しないと大変なことになります
for i in range(len(data)-1, -1, -1):
#小さい字を大きくする
data[i] = data[i].replace('ァ', 'ア')
data[i] = data[i].replace('ィ', 'イ')
data[i] = data[i].replace('ゥ', 'ウ')
data[i] = data[i].replace('ェ', 'エ')
data[i] = data[i].replace('ォ', 'オ')
data[i] = data[i].replace('ッ', 'ツ')
data[i] = data[i].replace('ャ', 'ヤ')
data[i] = data[i].replace('ュ', 'ユ')
data[i] = data[i].replace('ョ', 'ヨ')
#語尾の長音を削除
if data[i][-1] == 'ー':
data[i] = data[i][:-1]
#語尾が「ん」のポケモンを削除
if data[i][-1] == 'ン':
data.pop(i)
print('ポケモンの数:{}'.format(len(data)))
print('途中の8匹:{}'.format(data[3:11]))ポケモンの数:703
途中の8匹:['ヒトカゲ', 'リザード', 'ゼニガメ', 'カメール', 'カメツクス', 'キヤタピ', 'トランセル', 'バタフリ']語尾が「ん」のポケモンを除くと703匹でした。しりとりでどれくらい繋がるか楽しみです。途中の8匹を確認すると、リザードの後の「リザードン」が除かれていて、キャタピーが「キヤタピ」になっていますので、うまく処理できていることが分かります。
圧縮データの作成
評価関数の中でしりとりを行うのですが、Pythonの強みを活かせるように、頭文字の配列とお尻文字の配列を作っておきます。これを用意しておくと、しりとりが繋がっているかどうかを配列ごと一撃であぶり出すことができます。
#============================
#圧縮データの作成
#============================
#頭文字とお尻文字だけのデータ
head = []
tail = []
for a in data:
head.append(a[0])
tail.append(a[-1])
#後の処理のためにndarrayにしておきます
data = np.array(data)
data_save = np.array(data_save)
head = np.array(head)
tail = np.array(tail)
print('最初の4匹:{}'.format(data[:4]))
print('最初の4匹の頭文字:{}'.format(head[:4]))
print('最初の4匹のお尻文字:{}'.format(tail[:4]))
#151匹に限定
data = data[:123]
print('最後の3匹:{}'.format(data[-3:]))最初の4匹:['フシギダネ' 'フシギソウ' 'フシギバナ' 'ヒトカゲ']
最初の4匹の頭文字:['フ' 'フ' 'フ' 'ヒ']
最初の4匹のお尻文字:['ネ' 'ウ' 'ナ' 'ゲ']
最後の3匹:['カイリユ' 'ミユウツ' 'ミユウ']うまくできています。
(必須)評価関数
ポケモンIDが並んだparaを受け取って、しりとりを行います。先ほど言及したように、maskという配列はしりとりで「前後が接続しているか」を表すbool配列です。このmaskの中でTrueの最長継続数を数えてスコアとしたいです。
しかし、最長継続数をそのままスコアにすると離散的すぎてうまくGAが進みません。そこで、全体の中で何%が継続しているか(細かな鎖がどれくらいできているか)を小数の位に加えることにします。例えば、スコア8.2は最大接続数8、すべての接続点のうち20%が鎖を成していることを意味します。最大接続数が同じ8であっても、8.2の個体よりも8.3の個体のほうが、細かな鎖がたくさんできていて有望と判断されます。
#評価関数
def pokemon_score(para):
#頭文字配列とお尻文字配列をpara順に並び替える
head_para = head[para]
tail_para = tail[para]
#後ろと接続しているかどうかのbool配列(長さはdataより1短い)
mask = (head_para[1:] == tail_para[:-1])
#最長の接続数を計算
count = 0
max_count = 0
for i in range(len(mask)):
#継続していればカウント+1
if mask[i] == True:
count += 1
#継続していなければカウントリセット
else:
if count > max_count:
max_count = count
count = 0
#スコアを返す、例えば8.2であれば最長継続数8、全体の中での継続率20%を意味する
return max_count + (np.sum(mask) / len(mask))
print(data[10], data[4], data[66], data[18], data[0])
print(pokemon_score([10, 4, 66, 18, 0]))バタフリ リザード ドードリオ オニドリル フシギダネ
3.75試しにpara=[10, 4, 66, 18, 0]を入力してみると、スコア3.75が返ってきました。これは最大接続数が3であり、すべての接続点のうち75%が繋がっていることを意味します。
(任意)すべてのパラメータ群を可視化する関数
poolを受け取って、全員のスコアを計算し、棒グラフで表示します。
#poolの可視化
def pokemon_show_pool(pool, **info):
#任意で次の変数が使用できます
gen = info['gen']
best_index = info['best_index']
best_score = info['best_score']
mean_score = info['mean_score']
#mean_gap = info['mean_gap']
time = info['time']
#pool全員のスコアを計算
scores = []
for i in range(len(pool)):
scores.append(pokemon_score(pool[i]))
#エリートを表示
#print(pool[best_index])
#プロット
plt.figure(figsize=(6, 6))
plt.bar(range(len(pool)), scores)
plt.ylim([0, 30])
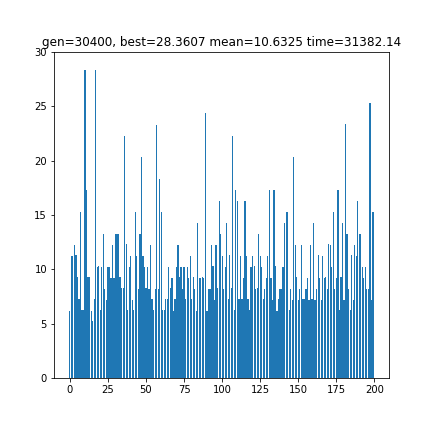
plt.title('gen={}, best={} mean={} time={}'.format(gen, best_score, mean_score, time))
#plt.savefig('save/{}.png'.format(gen))
plt.show()
print()GAで最適化(151匹)
151匹でやってみましょう。語尾「ん」を除くと123匹です。並び替え問題のためのtspGAを実行します。後半はしりとりを再現するための処理です。
#パラメータ範囲
para_range = np.arange(len(data))
#GAで最適化
para, score = vcopt().tspGA(para_range, #para_range
pokemon_score, #score_func
9999, #aim
show_pool_func=pokemon_show_pool, #show_para_func=None
seed=None, #seed=None
pool_num=100)
#結果の表示
print(para)
print(score)
#しりとり部分を再現
head_para = head[para]
tail_para = tail[para]
mask = (head_para[1:] == tail_para[:-1])
name = data_save[para]
count = 0
max_count = 0
for i in range(len(mask)):
if mask[i] == True:
count += 1
else:
if count > max_count:
max_count = count
words = name[i - count + 1: i + 1]
count = 0
#しりとりを表示
print(words)実行結果
[ 91 25 5 52 26 90 16 79 87 74 114 105 97 76 100 10 4 65
57 72 82 88 77 35 20 34 80 107 31 9 98 22 46 73 38 51
102 69 96 66 17 56 44 120 50 101 47 60 15 33 23 8 103 3
68 71 41 61 116 39 45 106 75 115 49 58 109 78 54 104 95 122
83 84 43 42 89 117 7 13 6 40 64 14 99 53 27 63 112 1
18 108 37 119 29 21 30 92 2 86 0 85 67 48 94 113 121 111
19 62 32 59 110 36 70 12 24 118 55 93 28 11 81]
28.360655737704917
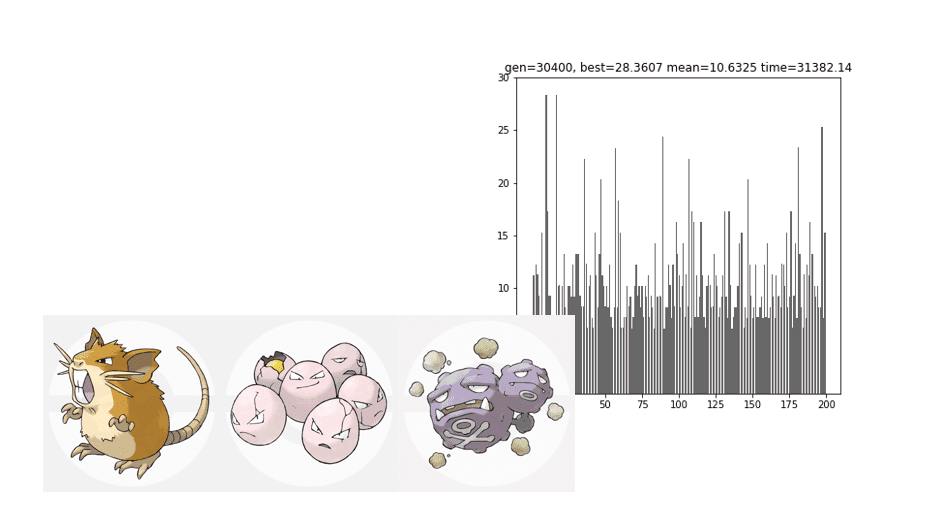
['ラッタ' 'タマタマ' 'マタドガス' 'スリープ' 'プテラ' 'ラプラス' 'ストライク' 'クラブ' 'ブーバー' 'バタフリー'
'リザード' 'ドードー' 'ドククラゲ' 'ゲンガー' 'ガラガラ' 'ラッキー' 'キングラー' 'ラフレシア' 'アーボック'
'クサイハナ' 'ナッシー' 'シャワーズ' 'ズバット' 'トランセル' 'ルージュラ' 'ライチュウ' 'ウインディ' 'イワーク']123匹全部の順番が返ってきましたが、どこかに28匹繋がっている部分があり、それをポケモン名で表示しました。また、全体のうち36%が大小いずれかの鎖の形成に携わっています。最後はイワークですが、「ク…ン」のポケモンはいませんので、29匹にはなりませんね。理論的には最長46という情報があります(参考文献の動画)ので、ちょっとイマイチですね。
703匹でやらないんですか?
いまのtspGA()は十分に高速化できていませんので、ちょっと厳しそうです。アップデートにご期待ください(するとは言っていない)。