やること
暗号化の最小コードをPythonで実装しながら、最終的にエニグマを作ることを目指すシリーズ。前回はシーザー暗号とヴィジュネル暗号を学びました。
今回はエニグマのアルゴリズムのエッセンスを学びます。
参考文献
手計算でエニグマを再現するキットが理解の助けになります


エニグマ(その1)
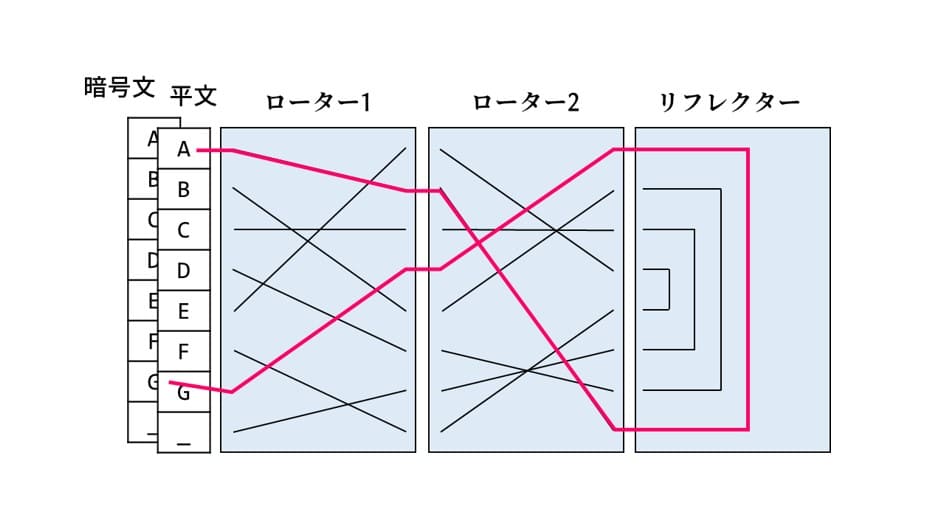
エニグマの仕組みを調べるとなにやら「プラグボード」「ローター(またはスクランブラー)」「リフレクター」という部分があることが分かります。エニグマの本質は「ローター」ですので、まずはこの部分を実装してみましょう。
ローター内部は、入力されたアルファベットを別のアルファベットに変換するように配線されています。シーザー暗号は+1とか+2とかキレイにシフトさせましたが、ローターはぐちゃぐちゃに変換します。でもやってることは同じ。頻度分析で解けます。
しかしこのローターは、1文字入力される度にギア1つ分回転します。つまり、文字毎にシフト量(というかシフト変換表)が変わります。これはまさにヴィジュネル暗号のエッセンスです。
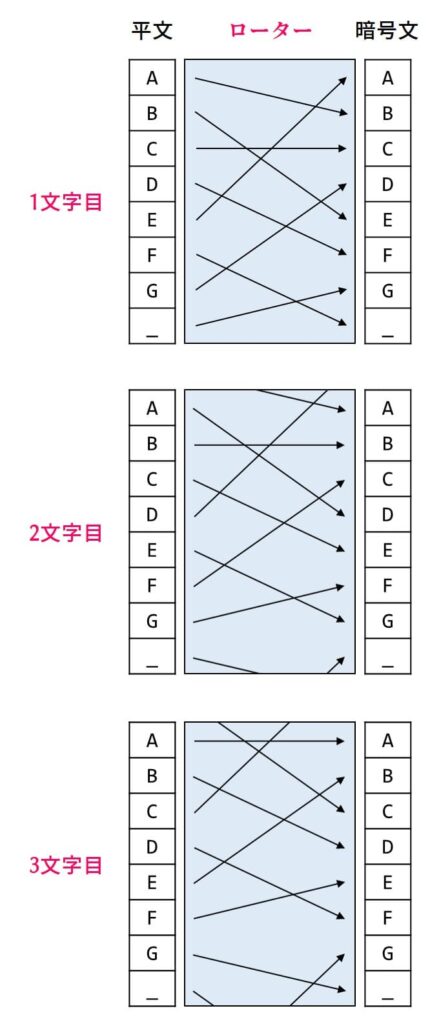

上のイラストは次のコードに対応しています。
'''
これまでの知識を使ってエニグマっぽいものを書く
ローター1枚のみ
'''
#文字テーブル
table = 'ABCDEFG_'
#ローター
rotor = [1, 3, 0, 2, 4, 2, 5, 7] #各文字のシフト量テーブル
#暗号化関数
def encrypt(word):
#暗号文初期化
ret = ''
for i, w in enumerate(word):
#文字→インデックス
index = table.index(w)
#ローター
#回転量
rot = i % 8
#回転したローター
rotor_rot = rotor.copy()
rotor_rot = np.roll(rotor_rot, -rot)
#シフト量
shift = rotor_rot[index]
#シフト
index = (index + shift) % 8
#インデックス→文字
ret += table[index]
return ret
print(encrypt('EGG_CAFE'))AF___C_G最初の3文字だけ丁寧に見ると、まず「E」→「A」に変換されます。ローターが回り「G」→「F」に。またローターが回り「G」→「_」に。目が疲れるのでこの辺にしておきましょう。
実は、これはまだエニグマの本質ではありません。この方法は周期8のヴィジュネル暗号みたいなもので、8文字毎に取り出して頻度分析すると解読できます。
エニグマ(その2)
ということでここからが本番です。
複数枚のローター
エニグマでは入力信号が3枚のローターを通過します。ここでは簡略化して2枚だけ書いてみます。
ローター1は文字を打つ度にギアが一つ回転します。ローター1が一周するとローター2のギアが一つ回転します。すなわち、2枚のローターによって周期が 82=64 になるということです。実際のエニグマではギア数が26(=アルファベットの数)なので周期が 263=17576 です。 指数関数!
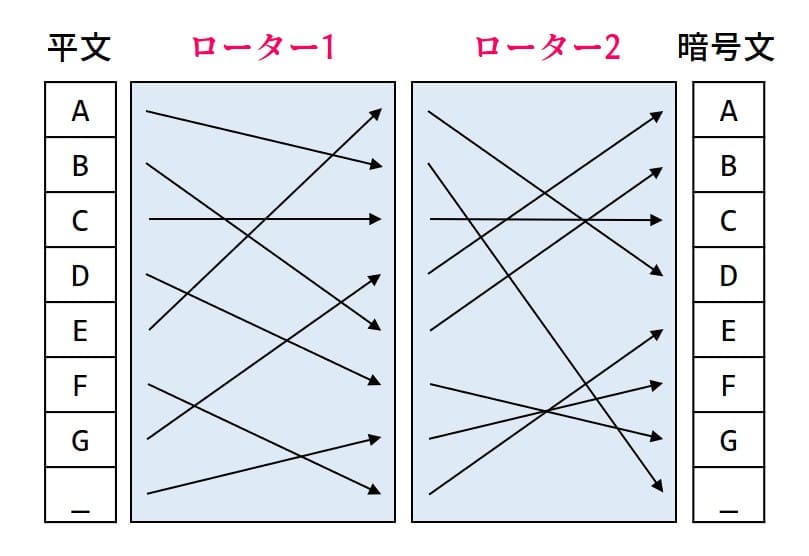

前回、
あ~あ、周期が無限大のヴィジュネル暗号があったらなぁ~
という声が聞こえていました。周期17576というのは、頻度分析で解こうとすると暗号文全体で数百万~数千万文字必要になります。そんなに長い文章は伝達しないし、ある程度長くなってきたらローターの設定(=鍵)を変えてしまえばいいのです。これがエニグマの堅牢性です。
リフレクター
ここでさらに「リフレクター」によって面白い工夫がなされています。リフレクターは一番奥で信号を変換・跳ね返して再度ローターに通す役割をもっています(回転はしません)。これにより暗号文は手前側で観測される形になります。
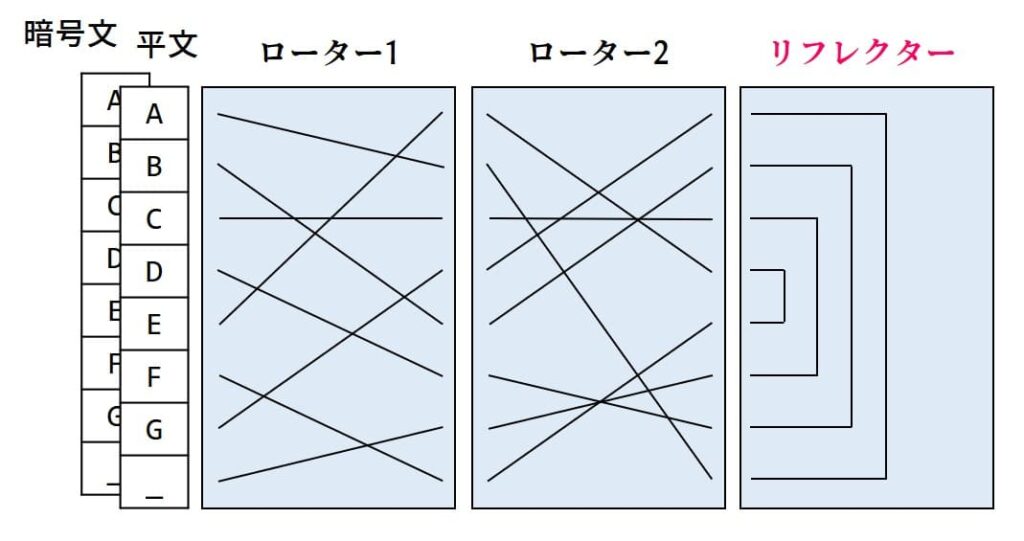

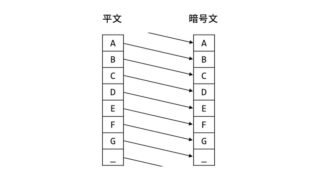
なぜわざわざこんなことをするのでしょうか。次の図を見てみます。平文で「A」を入力すると暗号文の「G」に変換されます。ここで気がついたでしょうか。平文として「G」を入力すると「A」が出てきます。
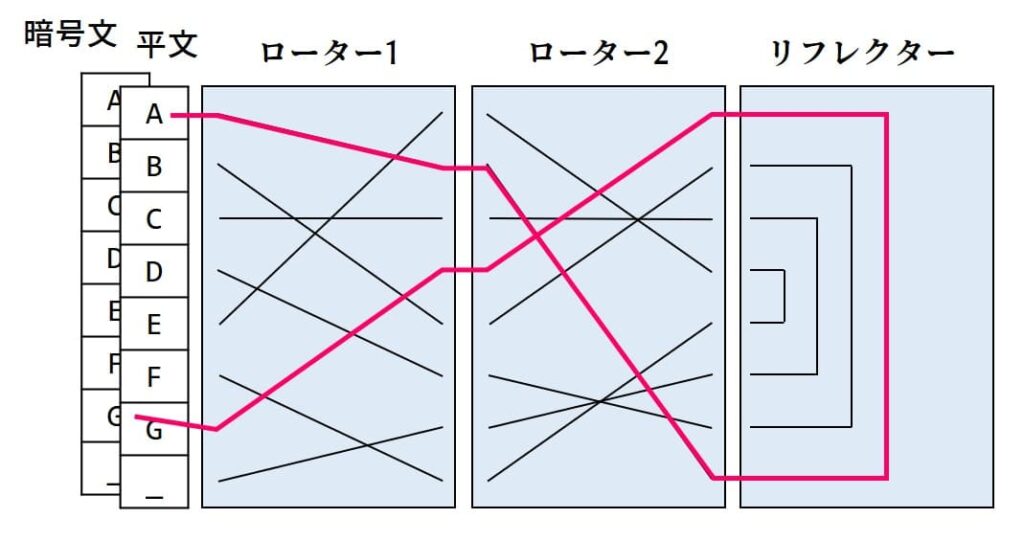

実はこれは画期的なことで、暗号化と復号が「同じマシン」「同じ設定」「同じ操作」で行えるのです。思い返せばシーザー暗号は、暗号化では+1シフト、復号では-1シフトさせる必要がありました。暗号化と復号で異なるマシン(もしくは異なる設定や操作)が必要なのです。ヴィジュネル暗号も同様です。これでは「あれ、なんかうまく復号できないな…」「お前の設定、逆じゃね?」「え、どっち?右?」「違う、お前から見て左!」みたいな問題が起きてしまいます(たぶん)。
ところがエニグマではリフレクターの実装により、暗号の送信者も受信者もまったく同じ設定を共有すればよいことになります。操作がとてもシンプルで初心者にも扱いやすい。これは運用上の大きなメリットだったそうです。
コード
はい、話が長くなりましたが以上がエニグマの本質ですので、少し大変ですが実装してみましょう。パラメータとしてローターに初期回転も与えてしまいます。リフレクターは暗号の堅牢性に寄与しないのですがロマンなので含めることにします。
'''
エニグマの最小構成
ローター2枚と初期回転を設定
'''
#文字テーブル
table = 'ABCDEFG_'
#ローター1
rotor1 = [1, 3, 0, 2, 4, 2, 5, 7] #信号のシフト量テーブル
init1 = 1
#ローター2
rotor2 = [3, 6, 0, 5, 5, 1, 7, 5] #信号のシフト量テーブル
init2 = 2
#リフレクター
reflector = [7, 6, 5, 4, 3, 2, 1, 0] #信号の変換テーブル
#暗号化関数
def encrypt(word):
#暗号文初期化
ret = ''
for i, w in enumerate(word):
#文字→インデックス
index = table.index(w)
#ローター1(順方向)
#回転量
rot = (init1 + i) % 8
#回転したローター
rotor1_rot = rotor1.copy()
rotor1_rot = np.roll(rotor1_rot, -rot)
#シフト量
shift = rotor1_rot[index]
#シフト
index = (index + shift) % 8
#ローター2(順方向)
#回転量
rot = (init2 + (i // 8)) % 8
#回転したローター
rotor2_rot = rotor2.copy()
rotor2_rot = np.roll(rotor2_rot, -rot)
#シフト量
shift = rotor2_rot[index]
#シフト
index = (index + shift) % 8
#リフレクターによる変換
index = reflector[index]
#ローター2(逆方向)
#逆転ローター
aim = (np.arange(8) + rotor2_rot) % 8
rotor2_rev = -rotor2_rot[np.argsort(aim)]
#シフト量
shift = rotor2_rev[index]
#シフト
index = (index + shift) % 8
#ローター1(逆方向)
#逆転ローター
aim = (np.arange(8) + rotor1_rot) % 8
rotor1_rev = -rotor1_rot[np.argsort(aim)]
#シフト量
shift = rotor1_rev[index]
#シフト
index = (index + shift) % 8
#インデックス→文字
ret += table[index]
return ret
print('暗号化')
print(encrypt('EGG_CAFE'))
print(encrypt('A_CAGED_BAD_DAD_FACED_A_CABBAGE_FED_AGED_BEEF'))暗号化
BDFGBFEC
CAEBAC_ACBEACFGCEEEC_BCCGBCFC_AFGB_BFA_CGEGFG「EGG_CAFE」が「BDFGBFEC」に変換されました。また、長い文章として「A caged bad dad faced a cabbage fed aged beef」も変換してみました。
さあ、ここからが注目です。暗号文をもう一度エニグマ(初期設定)に入力してみます。
print('復号')
print(encrypt('BDFGBFEC'))
print(encrypt('CAEBAC_ACBEACFGCEEEC_BCCGBCFC_AFGB_BFA_CGEGFG'))復号
EGG_CAFE
A_CAGED_BAD_DAD_FACED_A_CABBAGE_FED_AGED_BEEFきちんと平文が復元されました!
送信者はエニグマを初期設定にしてから平文を入力し、出てきた暗号文を無線で伝達します。受信者もエニグマを初期設定にして暗号文を打ち込み、平文を得ます。つまりエニグマは暗号化マシン兼復号マシンなのです。
これがエニグマの威力です。すごい! (≧∇≦*)
おわりに
ようやくエニグマの核心を理解することができました。ちなみに今回触れなかった「プラグボード」は組み合わせを増やすための追加ギミックのようです。
ここまで読んでくれたご褒美として「檻に囚われた悪徳親父がキャベツで育てられた熟成肉と対峙する」のイメージを置いておきますね。ABCDEFG_だけで作りました。ここで著作権を主張しておきます(え)


③運用考察編に続きます。