やること
機械学習による回帰の備忘録です。
- 正解モデルを定義
- 訓練データを生成
- 回帰学習(XGboost / ランダムフォレスト)
- 推定精度の確認
一連の流れを残しておきます。訓練データ生成のときにランダムなノイズを乗せることで回帰の効果を確認できます。今回はノイズは乗せず、正解モデルにどれだけ近い推定結果が得られるかだけ確認します。
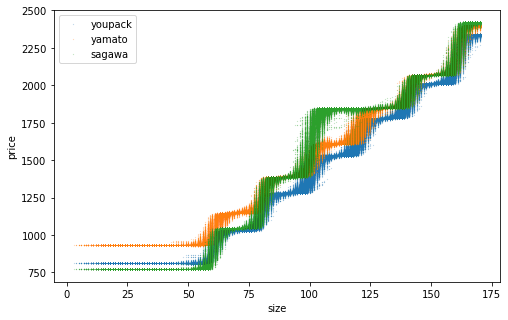
学習対象として「ゆうパック」「ヤマト宅急便」「佐川急便」の東京から東京へのサイズ別運賃を用います。たて、よこ、高さ、配送方法の4つを入力(説明変数)、運賃を出力(目的変数)として学習します。
参考文献
ゆうパックの運賃

ヤマトの運賃

佐川の運賃

XGBoostの使い方

エンコーディングのお勉強
機械学習の入力に離散値(離散ラベル)が含まれる場合、これをどうやって入れるかが問題になります。専門用語でエンコーディング方法と呼ばれます。
One-Hotエンコーディングについて(+多重共線性への対応)


決定木モデルにおけるラベルエンコーディングとOne-Hotエンコーディングの違いについて

離散ラベルに0, 1, 2, …と番号を当てて1列として入れるのがラベルエンコーディング。簡単でメモリの節約になるが、数量的な差を持たないラベルたち(例:犬、猿、雉)に数量関係を持たせてしまうため、できればOne-Hotエンコーディングしたほうが良い。ただし例外が2つある。離散ラベルではあるが数量的な意味を持っていると解釈できる場合(例:子供、大人、高齢者)はその順番でラベルを当てても良いだろう。また、決定木ベースの学習モデルを使用する場合(例:ランダムフォレスト、LightGBM)はラベルエンコーディングでも良い。だいたいこんな感じらしい。
実行環境
WinPython3.6をおすすめしています。

Google Colaboratoryが利用可能です。

正解モデルの定義
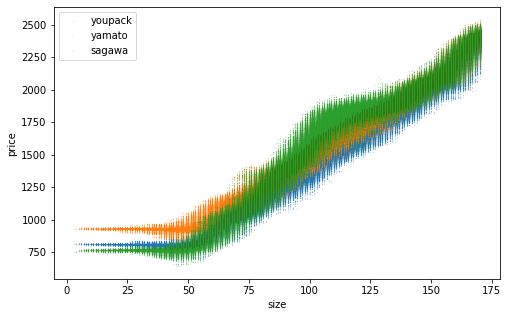
3つの配送方法の料金体系を書いてグラフにプロットします。サイズは10~170まで10刻みです。
import itertools
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import xgboost as xgb
#正解モデルを定義
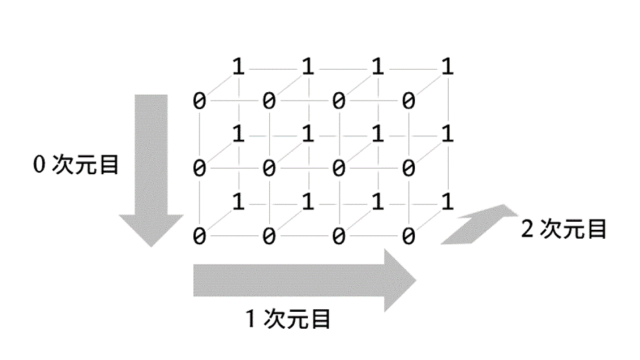
#マトリックスは1次元目:サービス名(ゆうパック、ヤマト、佐川) 2次元目:サイズ(10~170サイズまで10刻み)
service_names = ['youpack', 'yamato', 'sagawa']
price_range = range(10, 171, 10)
matrix = {'youpack':[810, 810, 810, 810, 810, 810, 1030, 1030, 1280, 1280, 1530, 1530, 1780, 1780, 2010, 2010, 2340],
'yamato':[930, 930, 930, 930, 930, 930, 1150, 1150, 1390, 1390, 1610, 1610, 1850, 1850, 2070, 2070, 2400],
'sagawa':[770, 770, 770, 770, 770, 770, 1045, 1045, 1386, 1386, 1848, 1848, 1848, 1848, 2068, 2068, 2420]}
#確認
plt.plot(price_range, matrix['youpack'], '--o', label='youpack')
plt.plot(price_range, matrix['yamato'], '--o', label='yamato')
plt.plot(price_range, matrix['sagawa'], '--o', label='sagawa')
plt.xlabel('size')
plt.ylabel('price')
plt.legend()
plt.show()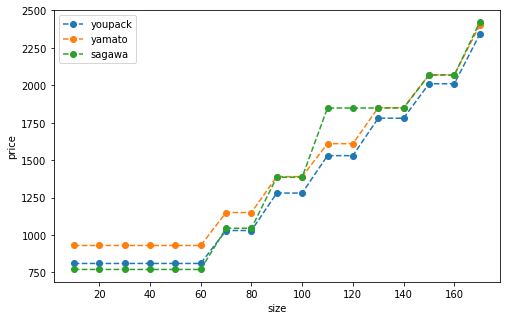
見やすいように点線で繋いでいますが、実際には階段状にガクガク上がります。佐川の大胆な一段飛ばしを覚えておいてください。
訓練データの生成
訓練データを1000個(1000行)生成します。
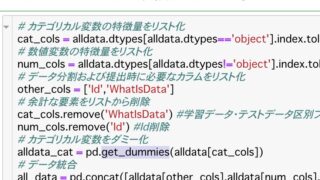
入力(x_train)は荷物の「たて」「よこ」「高さ」「配送方法」の4情報を持ちます。配送方法は多重共線性対応ということで3列ではなく2列のOne-Hotとし、したがって入力配列は5列です。
出力(y_train)は「料金」で、たて+よこ+高さ=サイズの概念を用いて算出されます。サイズ自体は列として入力しないため、機械学習によってサイズの概念を学習できるかどうかが本質的な焦点です。
#訓練データ作成
#入力(説明変数)のデータは 1列目:たて 2列目:よこ 3列目:高さ 4~6列目:サービスのワンホット([1, 0]='youpack', [0, 1]='yamato', [0, 0]='sagawa')
#出力(目的変数)のデータは 1列目:料金
x_train = []
y_train = []
num = 1000
while 1:
#たて、よこ、高さ生成
tate = nr.randint(1, 81)
yoko = nr.randint(1, 81)
height = nr.randint(1, 81)
#サイズ
size = tate + yoko + height
#サイズが170を超えたらやり直し
if size > 170:
continue
#サービス生成
service_name = nr.choice(service_names)
#料金
size_id = (size - 1) // 10
price = matrix[service_name][size_id]
#格納
if service_name == 'youpack':
x_train.append([tate, yoko, height, 1, 0])
if service_name == 'yamato':
x_train.append([tate, yoko, height, 0, 1])
if service_name == 'sagawa':
x_train.append([tate, yoko, height, 0, 0])
y_train.append(price)
if len(x_train) >= num:
break
x_train = np.array(x_train)
y_train = np.array(y_train)
print(x_train[:5])
print(y_train[:5])
#確認(ただしサイズの概念を使って)
plt.plot(np.sum(x_train[x_train[:, 3]==1, :3], axis=1), y_train[x_train[:, 3]==1], 'o', label='youpack')
plt.plot(np.sum(x_train[x_train[:, 4]==1, :3], axis=1), y_train[x_train[:, 4]==1], 'o', label='yamato')
plt.plot(np.sum(x_train[(x_train[:, 3]==0) & (x_train[:, 4]==0), :3], axis=1), y_train[(x_train[:, 3]==0) & (x_train[:, 4]==0)], 'o', label='sagawa')
plt.xlabel('size')
plt.ylabel('price')
plt.legend()
plt.show()[[57 78 13 0 0]
[42 38 16 1 0]
[64 32 5 1 0]
[53 68 23 0 1]
[62 72 19 0 1]]
[2068 1280 1530 2070 2070]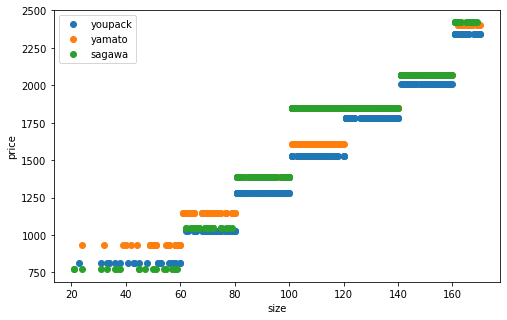
階段状です。
回帰学習(XGboost)
ここまでに用意したデータを7:3に分けて改めて「訓練データ」「テストデータ」と呼ぶことにします。
XGboostはほぼデフォルト設定ですが、max_depth=6→10に増やし、学習イテレーションを9999に増やしてearly_stoppingを加えました。
#訓練データ分割
x_train, x_test, y_train, y_test = train_test_split(x_train, y_train, test_size=0.3)
print(x_train.shape, x_test.shape, y_train.shape, y_test.shape)
#XGboostで回帰学習
model = xgb.XGBRegressor(n_estimators=9999, max_depth=10)
model.fit(x_train, y_train, eval_set=[(x_test, y_test)], early_stopping_rounds=10)(700, 5) (300, 5) (700,) (300,)
[0] validation_0-rmse:1185.65784
[1] validation_0-rmse:835.15094
[2] validation_0-rmse:596.64056
[3] validation_0-rmse:424.44379
[4] validation_0-rmse:307.71317
[5] validation_0-rmse:232.84102
[6] validation_0-rmse:184.68457
[7] validation_0-rmse:155.06062
[8] validation_0-rmse:138.36301
[9] validation_0-rmse:130.39771
[10] validation_0-rmse:126.12363
[11] validation_0-rmse:125.97745
[12] validation_0-rmse:126.16894
[13] validation_0-rmse:126.42770
[14] validation_0-rmse:127.37331
[15] validation_0-rmse:127.98996
[16] validation_0-rmse:128.67091
[17] validation_0-rmse:129.10474
[18] validation_0-rmse:129.12907
[19] validation_0-rmse:129.30972
[20] validation_0-rmse:129.33725
[21] validation_0-rmse:129.36194推定精度の確認
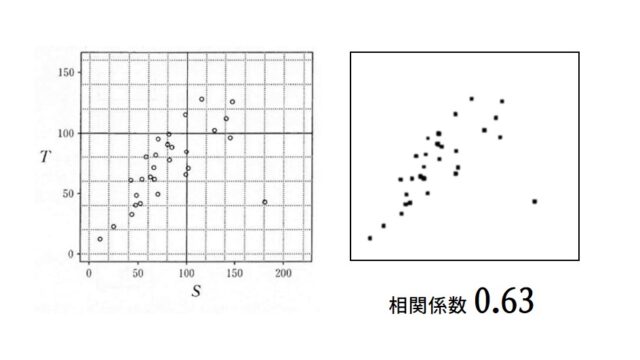
テストデータの正解と推定をプロット。相関係数も出します。
#相関確認
print('相関係数')
print(np.corrcoef(y_test, y_pred))
plt.plot(y_test, y_pred, 'o')
plt.xlabel('y_test')
plt.ylabel('y_pred')
plt.show()相関係数
[[1. 0.94975516]
[0.94975516 1. ]]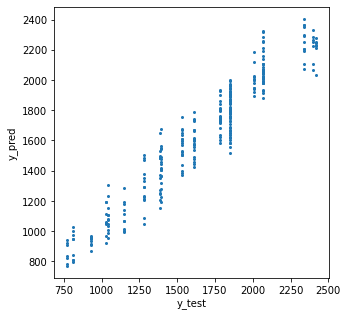
相関係数は0.95程度。
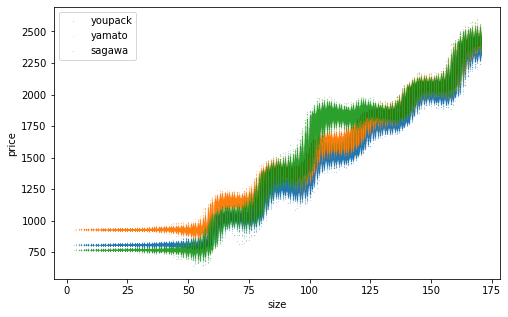
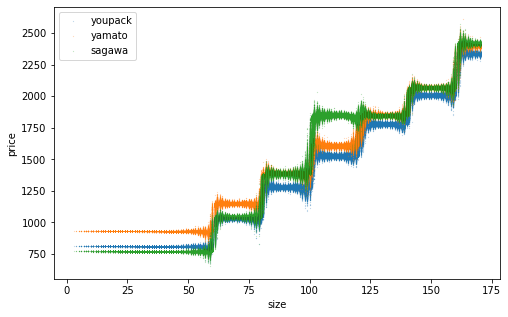
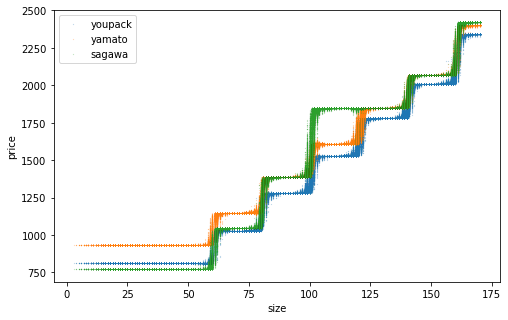
網羅的なデータを生成して推定精度を確認。訓練データ数を変えた結果を並べます。横軸は「サイズ」であることに注意。推定した点が上下にブレているのは、同じサイズでも元となるたて・よこ・高さが異なり推定結果が異なるため。訓練データ数を増やすほどそのブレが小さくなり、佐川の一段飛ばしもはっきりと表現できるようになりました。
#網羅的なデータで推定してみる
for b1, b2, service_name in [[1, 0, 'youpack'], [0, 1, 'yamato'], [0, 0, 'sagawa']]:
#x生成
x = itertools.product(np.arange(1, 81), np.arange(1, 81), np.arange(1, 81), [b1], [b2])
x = np.array(list(x))
x = x[np.sum(x[:, :3], axis=1) <= 170]
#料金推定
price_pred = model.predict(x)
#グラフ
plt.plot(np.sum(x[:, :3], axis=1), price_pred, 'o', label=service_name)
plt.xlabel('size')
plt.ylabel('price')
plt.legend()
plt.show()
n=1000 
n=10000 
n=100000 
n=1000000
ランダムフォレストの場合
途中を少し変えるだけです。ランダムフォレストにはイテレーションの概念がなく、テストデータを使用して学習経過を監視する必要がありません。勝手に停止します。学習時間はXGboostよりかなり短かったです。
from sklearn.ensemble import RandomForestRegressor
#ランダムフォレストで回帰学習
model = RandomForestRegressor()
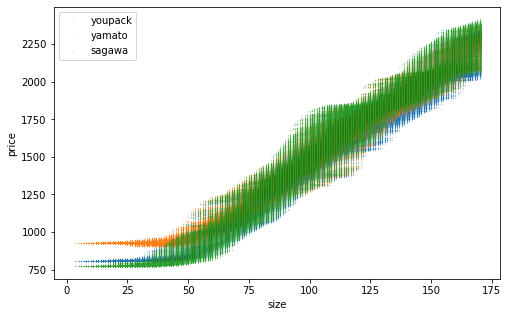
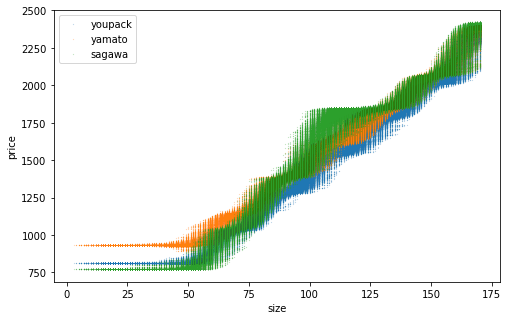
model.fit(x_train, y_train)訓練データ数を変えた学習結果がこちら。

n=1000 
n=10000 
n=100000 
n=1000000
おわりに
今回、訓練データの理論上の組み合わせ数は80×80×80×3=約150万通りです。訓練データ数が多いほど学習精度が良くなったのは、精度評価に使用したデータが訓練データに含まれていた影響が大きいと思います。きちんとやるなら、訓練データに含まれないデータをテストデータに用いて学習を監視し、評価にも用いた方が良いです。
今回はあまり回帰向きではない正解モデルを使用しました。階段状のモデルをどれだけ学習できるか興味があったからです。もっと回帰の効果を見るには、何か数式を用いたモデルにランダムノイズを乗せて学習するのが良いでしょう。